Каждую тригонометрическую функцию углов можно выразить через тригонометрическую функцию угла . Покажем это сначала для синусов и косинусов.
Вывод формул приведения
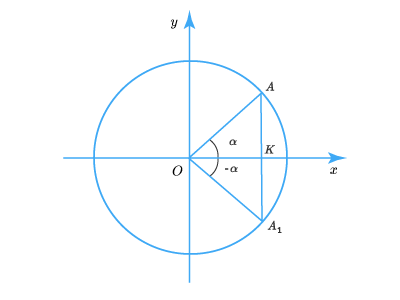
Пусть – произвольный угол, выраженный в радианах. На единичном круге ему соответствует определенная точка , а углу – точка :
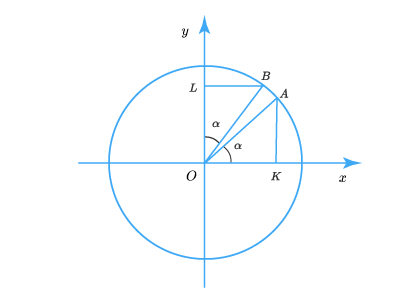
Опустив перпендикуляры на ось и на ось , получим два равных треугольника и L (так угол равен и ). Поэтому и , то есть , .
Углам и на единичной окружности соответствуют точки, симметричные относительно оси :
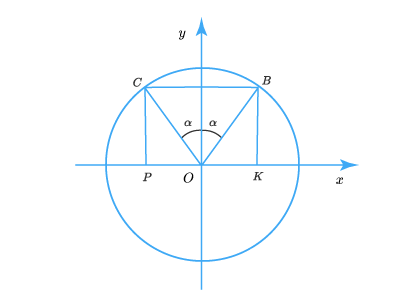
Их ординаты на уровне абсциссы противоположные. Поэтому , .
Углам и также соответствуют точки единичного круга, симметричные относительно оси :
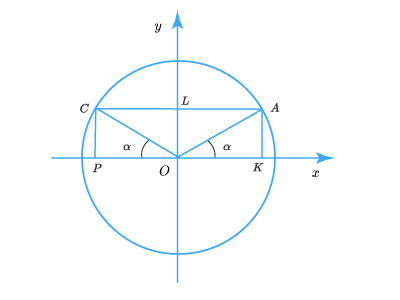
Поэтому .
Углам и (а также , , , ) соответствуют точки единичного круга, симметричные относительно начала координат:
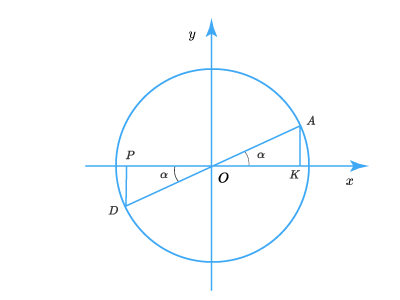
Их ординаты противоположные и абсциссы противоположные. Поэтому:
,
,
,
,
.
Углам и соответствуют точки единичного круга, симметричные относительно оси :
Их абсциссы находятся на одном уровне, а ординаты противоположны. Поэтому:
,
Углам и соответствует одна и та же точка единичного круга, поэтому , .
Из предыдущих рассуждений имеем 16 формул.
Еще 16 подобных формул можно доказать для тангенса и котангенса:
и т. д.
Все эти 32 формулы называют формулами приведения, потому что они дают возможность каждую тригонометрическую функцию произвольного угла (а следовательно - и числа) свести к тригонометрической функции острого угла.
Правило приведения
Запоминать каждую из этих формул нет необходимости, лучше пользоваться общим правилом.
Чтобы понятнее его сформулировать, договоримся синус считать кофункцией косинуса и наоборот, а тангенс – кофункцией котангенса и наоборот. Скажем также, что угол строящейся функции откладывается от горизонтального диаметра, если он имеет вид или , или от вертикального диаметра, если он имеет вид или .
Если угол строящейся тригонометрической функции откладывается от вертикального диаметра, то ее заменяют кофункцией, если же от горизонтального диаметра, то ее название не меняют. Знак ставим такой, который имеет значение строящейся функции при условии, что угол острый.
Пользуясь правилом сведения, мы только для удобства принимаем, что угол острый. На самом деле в каждой из формул сведения под переменной можно понимать и степень произвольного угла, в том числе отрицательного, и любое действительное число.
Формулам сведения можно отнести также тождества:
.
Не знаете, сколько стоит статья по математике на заказ? Обратитесь к нашим экспертам!



Комментарии