Мы уже знакомы с понятием определителя матрицы. Также мы рассмотрели правила вычисления детерминантов (определителей) первого и второго порядка. Познакомимся с различными вариантами нахождения определителей третьего порядка.
Вычисление определителей по правилу треугольника
Схематически раскрытие определителя по этому правилу выглядит так:
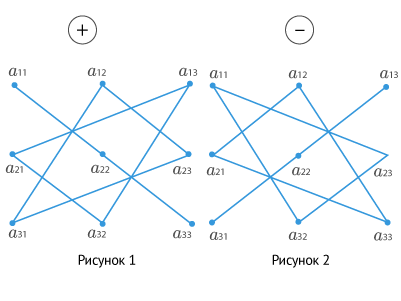
Согласно рисункам №1 и №2 мы перемножаем элементы, соединенные прямыми. Произведения элементов будут иметь определенные знаки: для рисунка 1 — «+», для рисунка 2 — «-».
| Произведения, которые берутся со знаком «+» |
Произведения, которые берутся со знаком «-» |
| a11 ⋅a22 ⋅a33 |
a13 ⋅a22 ⋅a31 |
| a12 ⋅a23 ⋅a31 |
a12 ⋅a33 ⋅a21 |
| a13 ⋅a32 ⋅a21 |
a11 ⋅a23 ⋅a32 |
На рисунке 1 мы видим равнобедренные треугольники с основаниями, параллельными главной диагонали; на рисунке 2 — равнобедренные треугольники с основаниями, параллельными второй (побочной) диагонали. Поэтому данное правило имеет такое название.
Определитель может быть вычислен по формуле:
∣∣∣∣∣∣ a11 a21 a31 a12 a22 a32 a13 a23 a33 ∣∣∣∣∣∣ =
=a11 ⋅a22 ⋅a33 +a12 ⋅a23 ⋅a31 +a13 ⋅a32 ⋅a21 −a13 ⋅a22 ⋅a31 −a12 ⋅a33 ⋅a21 −a11 ⋅a23 ⋅a32 .
Примеры
Рассмотрим примеры нахождения определителя по правилу треугольника.
Найти определитель ∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ по правилу треугольника.
По правилу треугольника определитель третьего порядка равен:
∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =9⋅4⋅7+2⋅8⋅6+5⋅3⋅1−5⋅4⋅6−2⋅7⋅1−9⋅8⋅3=
=252+96+15−120−14−216=13.
Найти определитель ∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ по правилу треугольника.
Искомый определитель третьего порядка равен:
∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =
=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅0⋅6−(−4)⋅(−3)⋅1−1⋅(−1)⋅6−2⋅5⋅0=6+5−12+6=5.
При вычислении определителей таким способом можно легко совершить ошибку из-за невнимательности. Чтобы избежать таких ошибок существует второй способ, называемый правилом Саррюса, или способом «параллельных полосок».
Вычисление определителей по правилу Саррюса
Правило Саррюса также именуют способом присоединения двух строк/столбцов или правилом параллельных полосок.
Основная идея этого правила состоит в приписывании первого и второго столбца справа от определителя.
Вычисления будем производить по следующей схеме:
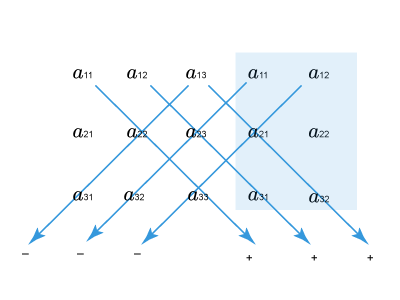
Перемножаем элементы, соединенные прямыми. Данные произведения берем со знаком «+», если диагональ, на которой они стоят, является главной или параллельной ей; со знаком «-», если она является второй (побочной) или параллельной ей.
| Произведения, которые берутся со знаком «+» |
Произведения, которые берутся со знаком «-» |
| a11 ⋅a22 ⋅a33 |
a13 ⋅a22 ⋅a31 |
| a12 ⋅a23 ⋅a31 |
a11 ⋅a23 ⋅a32 |
| a13 ⋅a21 ⋅a32 |
a12 ⋅a21 ⋅a33 |
В общем виде вычисление по правилу Саррюса можно записать следующим образом:
∣∣∣∣∣∣ a11 a21 a31 a12 a22 a32 a13 a23 a33 ∣∣∣∣∣∣ =∣∣∣∣∣∣ a11 a21 a31 a12 a22 a32 a13 a23 a33 ∣∣∣∣∣∣ a11 a21 a31 a12 a22 a32 =
=a11 ⋅a22 ⋅a33 +a12 ⋅a23 ⋅a31 +a13 ⋅a21 ⋅a32 −a13 ⋅a22 ⋅a31 −a11 ⋅a23 ⋅a32 −a12 ⋅a21 ⋅a33 .
Сравнивая эти два способа вычисления определителей, видим одинаковые множители, которые во втором случае немного переставлены местами.
Возможность допустить ошибку, вычисляя определитель по правилу Саррюса, намного меньше.
Примеры
Найти определитель ∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ по правилу Саррюса.
Приписываем два первых столбца справа от определителя и вычисляем его:
∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ 916 243 =
=9⋅4⋅7+2⋅8⋅6+5⋅1⋅3−5⋅4⋅6−9⋅8⋅3−2⋅1⋅7=252+96+15−120−216−14=13.
Найти определитель ∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ по правилу Саррюса.
Приписываем два первых столбца справа от определителя и вычисляем его:
∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ 261 1−30 =
=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅6⋅0−(−4)⋅(−3)⋅1−2⋅5⋅0−1⋅6⋅(−1)=6+5−12+6=5.
Существует еще одна вариация правила Саррюса. Она состоит в приписывании первой и второй строки снизу от определителя. Вычисления производятся аналогично.
Минор и алгебраическое дополнение
Прежде чем перейти к рассмотрению еще одного способа вычисления определителей 3-го порядка разберем 2 понятия: минор, алгебраическое дополнение.
Минор
Минором Mij к элементу aij определителя n-го порядка называется определитель (n−1)-го порядка, который получается из исходного определителя вычеркиванием i-той строки и j-того столбца.
Таким образом, минор — это определитель, который остается после вычеркивания определенной строки и определенного столбца. Например, M11 получается вычеркиванием 1-й строки и 1-го столбца, M23 — вычеркиванием 2-й строки и 3-го столбца.
Алгоритм нахождения миноров:
- вычеркиваем i-ю строку;
- вычеркиваем j-й столбец;
- записываем определитель, который получили в результате действий 1 и 2.
Примеры
Найти миноры матрицы F=⎝⎛ 916 243 587 ⎠⎞ .
Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.
M11 =∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =∣∣∣∣ 43 87 ∣∣∣∣ =4⋅7−3⋅8=28−24=4,
M12 =∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =∣∣∣∣ 16 87 ∣∣∣∣ =1⋅7−6⋅8=7−48=−41,
M13 =∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =∣∣∣∣ 16 43 ∣∣∣∣ =1⋅3−6⋅4=3−24=−21,
M21 =∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =∣∣∣∣ 23 57 ∣∣∣∣ =2⋅7−3⋅5=14−15=−1,
M22 =∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =∣∣∣∣ 96 57 ∣∣∣∣ =9⋅7−6⋅5=63−30=33,
M23 =∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =∣∣∣∣ 96 23 ∣∣∣∣ =9⋅3−6⋅2=27−12=15,
M31 =∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =∣∣∣∣ 24 58 ∣∣∣∣ =2⋅8−4⋅5=16−20=−4,
M32 =∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =∣∣∣∣ 91 58 ∣∣∣∣ =9⋅8−1⋅5=72−5=67,
M33 =∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =∣∣∣∣ 91 24 ∣∣∣∣ =9⋅4−1⋅2=36−2=34.
Найти миноры матрицы G=⎝⎛ 261 1−30 −45−1 ⎠⎞ .
Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.
M11 =∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =∣∣∣∣ −30 5−1 ∣∣∣∣ =(−3)⋅(−1)−0⋅5=3−0=3,
M12 =∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =∣∣∣∣ 61 5−1 ∣∣∣∣ =6⋅(−1)−1⋅5=−6−5=−11,
M13 =∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =∣∣∣∣ 61 −30 ∣∣∣∣ =6⋅0−1⋅(−3)=0+3=3,
M21 =∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =∣∣∣∣ 10 −4−1 ∣∣∣∣ =1⋅(−1)−0⋅(−4)=−1−0=−1,
M22 =∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =∣∣∣∣ 21 −4−1 ∣∣∣∣ =2⋅(−1)−1⋅(−4)=−2+4=2,
M23 =∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =∣∣∣∣ 21 10 ∣∣∣∣ =2⋅0−1⋅1=0−1=−1,
M31 =∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =∣∣∣∣ 1−3 −45 ∣∣∣∣ =1⋅5−(−3)⋅(−4)=5−12=−7,
M32 =∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =∣∣∣∣ 26 −45 ∣∣∣∣ =2⋅5−6⋅(−4)=10+24=34,
M33 =∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =∣∣∣∣ 26 1−3 ∣∣∣∣ =2⋅(−3)−6⋅1=−6−6=−12.
Алгебраическое дополнение
Алгебраическое дополнение
Алгебраическим дополнением Aij к элементу aij определителя n-го порядка называется число Aij =(−1)i+j⋅Mij ,
где i, j — соответствующие строка и столбец,
Mij — минор к элементу aij .
Алгоритм нахождения алгебраических дополнений:
- найти сумму номеров строки (i) и столбца (j);
- найти минор Mij по алгоритму нахождения миноров, который представлен выше;
- подставить значения, полученные на шагах 1 и 2, в формулу Aij =(−1)i+j⋅Mij .
Примеры
Найти алгебраические дополнения матрицы F=⎝⎛ 916 243 587 ⎠⎞ .
A11 =(−1)1+1⋅M11 =(−1)2⋅∣∣∣∣ 43 87 ∣∣∣∣ =4,
A12 =(−1)1+2⋅M12 =(−1)3⋅∣∣∣∣ 16 87 ∣∣∣∣ =41,
A13 =(−1)1+3⋅M13 =(−1)4⋅∣∣∣∣ 16 43 ∣∣∣∣ =−21,
A21 =(−1)2+1⋅M21 =(−1)3⋅∣∣∣∣ 23 57 ∣∣∣∣ =1,
A22 =(−1)2+2⋅M22 =(−1)4⋅∣∣∣∣ 96 57 ∣∣∣∣ =33,
A23 =(−1)2+3⋅M23 =(−1)5⋅∣∣∣∣ 96 23 ∣∣∣∣ =−15,
A31 =(−1)3+1⋅M31 =(−1)4⋅∣∣∣∣ 24 58 ∣∣∣∣ =−4,
A32 =(−1)3+2⋅M32 =(−1)5⋅∣∣∣∣ 91 58 ∣∣∣∣ =−67,
A33 =(−1)3+3⋅M33 =(−1)6⋅∣∣∣∣ 91 24 ∣∣∣∣ =34.
Найти алгебраические дополнения матрицы G=⎝⎛ 261 1−30 −45−1 ⎠⎞ .
A11 =(−1)1+1⋅M11 =(−1)2⋅∣∣∣∣ −30 5−1 ∣∣∣∣ =3,
A12 =(−1)1+2⋅M12 =(−1)3⋅∣∣∣∣ 61 5−1 ∣∣∣∣ =11,
A13 =(−1)1+3⋅M13 =(−1)4⋅∣∣∣∣ 61 −30 ∣∣∣∣ =3,
A21 =(−1)2+1⋅M21 =(−1)3⋅∣∣∣∣ 10 −4−1 ∣∣∣∣ =1,
A22 =(−1)2+2⋅M22 =(−1)4⋅∣∣∣∣ 21 −4−1 ∣∣∣∣ =2,
A23 =(−1)2+3⋅M23 =(−1)5⋅∣∣∣∣ 21 10 ∣∣∣∣ =1,
A31 =(−1)3+1⋅M31 =(−1)4⋅∣∣∣∣ 1−3 −45 ∣∣∣∣ =−7,
A32 =(−1)3+2⋅M32 =(−1)5⋅∣∣∣∣ 26 −45 ∣∣∣∣ =−34,
A33 =(−1)3+3⋅M33 =(−1)6⋅∣∣∣∣ 26 1−3 ∣∣∣∣ =−12.
Зная, что такое миноры и алгебраические дополнения, рассмотрим вычисление определителя по строке и столбцу.
Вычисление определителя по строке или столбцу
Определитель матрицы равен сумме произведений элементов строки (столбца) на их алгебраические дополнения.
Алгоритм вычисления определителя по строке или столбцу:
- находим алгебраические дополнения элементов строки или столбца;
- находим произведения элементов на их алгебраические дополнения;
- находим сумму, полученных на шаге 2, произведений.
Примеры
Найти определитель ∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ по 2 столбцу.
∣∣∣∣∣∣ 916 243 587 ∣∣∣∣∣∣ =2⋅A12 +4⋅A22 +3⋅
A32 =2(−1)3M12 +4(−1)4M22 +3(−1)5M32 =2(−1)3∣∣∣∣ 16 87 ∣∣∣∣ +4(−1)4∣∣∣∣ 96 57 ∣∣∣∣ +3(−1)5∣∣∣∣ 91 58 ∣∣∣∣ =
=−2⋅(−41)+4⋅33−3⋅67=82+132−201=13.
Найти определитель ∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ по 3 строке.
∣∣∣∣∣∣ 261 1−30 −45−1 ∣∣∣∣∣∣ =1⋅A31 +0⋅A32 −1⋅A33 =1(−1)4M31 +0(−1)5M32 −1(−1)6M33 =
=1(−1)4∣∣∣∣ 1−3 −45 ∣∣∣∣ +0(−1)5∣∣∣∣ 26 −45 ∣∣∣∣ −1(−1)6∣∣∣∣ 26 1−3 ∣∣∣∣ =−7+0+12=5.
Любой из рассмотренных способов можно применять при нахождении определителей третьего порядка. В следующий раз мы разберем вычисление определителей матриц высших порядков.
На Студворк вы можете заказать статью по математике онлайн у профильных экспертов!
Тест по теме «Как вычислить определитель матрицы третьего порядка»





Комментарии