В прошлый раз мы рассмотрели понятие определителя матрицы. Для вычисления определителей существуют различные правила. Например, определитель матрицы первого порядка — элемент . Рассмотрим вычисление определителя второго порядка.
Для того чтобы вычислить определитель второго порядка необходимо из произведения элементов главной диагонали вычесть произведение элементов второй (побочной) диагонали.
В общем случае нахождение определителя выглядит следующим образом:
.
Схема вычисления определителя второго порядка выглядит следующим образом:
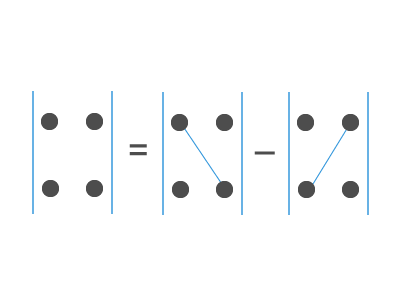
Алгоритм нахождения определителя второго порядка:
- Определяем порядок определителя (подробнее о порядке определителя можно узнать в теме «Что такое определитель матрицы»).
- Если порядок определителя = 2, то находим произведение элементов главной диагонали, и произведение элементов второй (побочной) диагонали (с понятием главной и побочной диагонали можно ознакомиться в теме «Основные типы матриц»).
- Находим разность произведения элементов главной диагонали и произведения элементов второй (побочной диагонали).
Вычислить определитель второго порядка .
Определитель второго порядка равен
.
Вычислить определитель второго порядка .
Определитель второго порядка равен .
На Студворк вы можете заказать статью по математике онлайн у профильных экспертов!



Комментарии