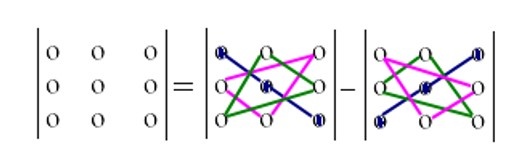
Это способ вычисления определителя матрицы, который включает в себя поиск по следующей схеме:
Онлайн-калькулятор
Как вы уже поняли, метод получил название правила треугольника из-за того, что умноженные элементы матрицы образуют вид треугольников.
Чтобы лучше это понять, давайте рассмотрим пример:
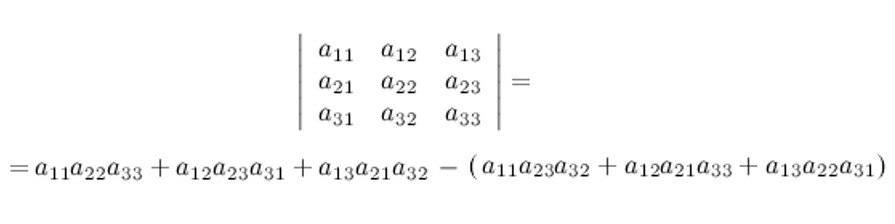
Теперь рассмотрим вычисление определителя матрицы с действительными числами по правилу треугольника.
Дано:
A=⎝⎛ 212125 121212 145614 ⎠⎞
Решение:
∣A∣=21⋅12⋅14+12⋅56⋅25+14⋅21⋅12−14⋅12⋅25−12⋅56⋅21−21⋅12⋅14=2016
Теперь данную матрицу перепишем и приравняем ее к определителю
∣A∣=⎝⎛ 212125 121212 145614 ⎠⎞ =2016
Вычислим более сложный пример.
Нам дано:
A=⎝⎛ 15256 405 42166 ⎠⎞
Требуется найти определитель методом треугольника.
Подставим данные в формулу:
∣A∣=15⋅0⋅166+4⋅2⋅56+4⋅2⋅5−4⋅0⋅56−5⋅2⋅15−2⋅4⋅166=−990
∣A∣=⎝⎛ 15256 405 42166 ⎠⎞ =−990
Итак, определитель матрицы равен -990.
Для общего понимания указанной темы вычислим определитель матрицы, где узлами являются дробные числа:
A=⎝⎛ 1216 82 212 2115 84 95 9914 514 1 ⎠⎞
Определим решение для данной матрицы:
∣A∣=1216 ⋅84 ⋅1+2115 ⋅514 ⋅212 +9914 ⋅82 ⋅95 −9914 ⋅84 ⋅212 −95 ⋅514 ⋅1216 −82 ⋅2115 ⋅1=24948249715
∣A∣=⎝⎛ 1216 82 212 2115 84 95 9914 514 1 ⎠⎞ =24948249715
Ответом станет ∣A∣=24948249715
На Студворк вы можете заказать статью по математике онлайн у профильных экспертов!
Тест по теме «Нахождение определителя методом треугольника»

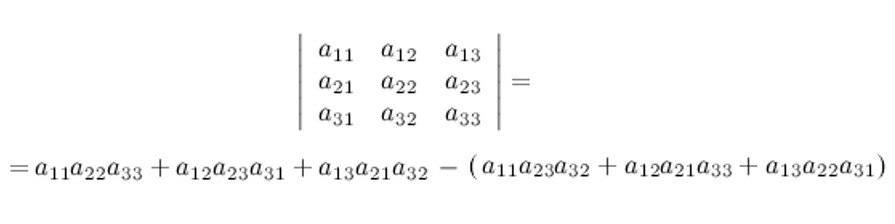



Комментарии