Перед тем как перейти к решению систем линейных уравнений методом обратной матрицы вспомним, что такое обратная матрица, какие способы ее нахождения существуют, что такое матричные уравнения и как они решаются.
Система линейных уравнений (СЛУ)
Под системой линейных уравнений (СЛУ) будем понимать систему ⎩⎪⎪⎪⎨⎪⎪⎪⎧ a11 x1 +a12 x2 +a13 x3 +…+a1n xn =b1 ,a21 x1 +a22 x2 +a23 x3 +…+a2n xn =b2 ,………………………………….am1 x1 +am2 x2 +am3 x3 +…+amn xn =bm . ,
содержащую m уравнений и n неизвестных.
Линейность означает, что все неизвестные в уравнении содержатся в первой степени.
Рассмотрим на схеме основные понятия, связанные с понятием системы линейных уравнений.
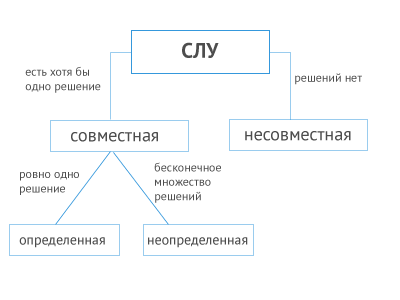
Матричная форма записи СЛУ
С каждой системой линейных уравнений
⎩⎪⎪⎪⎨⎪⎪⎪⎧ a11 x1 +a12 x2 +a13 x3 +…+a1n xn =b1 ,a21 x1 +a22 x2 +a23 x3 +…+a2n xn =b2 ,………………………………….am1 x1 +am2 x2 +am3 x3 +…+amn xn =bm . можно связать несколько матриц.
-
Матрица системы, состоящая из коэффициентов заданной системы линейных уравнений: A=⎝⎜⎜⎛ a11 a21 …am1 a12 a22 …am2 a13 a23 …am3 ………… a1n a2n …amn ⎠⎟⎟⎞ .
-
Матрица неизвестных, состоящая из столбца, который содержит неизвестные x1 ,x2 ,...,xn :
X=⎝⎜⎜⎛ x1 x2 ...xn ⎠⎟⎟⎞ .
- Матрица свободных членов, состоящая из столбца, который содержит свободные члены b1 ,b2 ,...,bm :
B=⎝⎜⎜⎛ b1 b2 ...bm ⎠⎟⎟⎞ .
Используя введенные обозначения (A — матрица системы, X — матрица неизвестных, B — матрица свободных членов) СЛУ можно записать в виде матричного уравнения A⋅X=B, поэтому метод обратной матрицы, по существу, является частным случаем матричного уравнения.
Метод обратной матрицы может применяться только для тех систем линейных уравнений, у которых определитель матрицы системы отличен от нуля, а именно ∣∣ A ∣∣ =0. Если же ∣∣ A ∣∣ =0, то решить СЛУ матричным методом невозможно (в таком случае СЛУ может быть решена методом Гаусса).
Алгоритм решения СЛУ методом обратной матрицы
- Записать систему линейных уравнений в матричной форме: A⋅X=B, где
A=⎝⎜⎜⎛ a11 a21 …am1 a12 a22 …am2 a13 a23 …am3 ………… a1n a2n …amn ⎠⎟⎟⎞ — матрица системы,
X=⎝⎜⎜⎛ x1 x2 ...xn ⎠⎟⎟⎞ — матрица неизвестных,
B=⎝⎜⎜⎛ b1 b2 ...bm ⎠⎟⎟⎞ — матрица свободных членов.
- Решить матричное уравнение A⋅X=B:
2.1 Найти обратную матрицу A−1 одним из способов.
2.2 Найти X, используя равенство X=⎝⎜⎜⎛ x1 x2 ...xn ⎠⎟⎟⎞ =A−1⋅B.
Рассмотрим примеры решения СЛУ методом обратной матрицы.
Пример 1
Решить систему ⎩⎪⎨⎪⎧ x1 −2x2 +x3 =1,2x1 −x2 +x3 =2,3x1 +2x2 +2x3 =−2. с помощью обратной матрицы.
Запишем систему в матричной форме A⋅X=B, где
A=⎝⎛ 123 −2−12 112 ⎠⎞ ,
X=⎝⎛ x1 x2 x3 ⎠⎞ ,
B=⎝⎛ 12−2 ⎠⎞ :
⎝⎛ 123 −2−12 112 ⎠⎞ ⋅⎝⎛ x1 x2 x3 ⎠⎞ =⎝⎛ 12−2 ⎠⎞ .
∣∣∣∣∣∣ 123 −2−12 112 ∣∣∣∣∣∣ =5 =0, значит, уравнение можно решить методом обратной матрицы.
Найдем обратную матрицу A−1 методом элементарных преобразований.
Составим расширенную матрицу:
⎝⎛ 123 −2−12 112 ∣∣∣∣∣∣ 100 010 001 ⎠⎞ .
Прибавим к строке №2 строку №1, умноженную на -2:
⎝⎛ 123 −2−12 112 ∣∣∣∣∣∣ 100 010 001 ⎠⎞ ∼⎝⎛ 103 −232 1−12 ∣∣∣∣∣∣ 1−20 010 001 ⎠⎞ .
Прибавим к строке №3 строку №1, умноженную на -3:
⎝⎛ 103 −232 1−12 ∣∣∣∣∣∣ 1−20 010 001 ⎠⎞ ∼⎝⎛ 100 −238 1−1−1 ∣∣∣∣∣∣ 1−2−3 010 001 ⎠⎞ .
Прибавим к строке №2 строку №3, умноженную на -1:
⎝⎛ 100 −238 1−1−1 ∣∣∣∣∣∣ 1−2−3 010 001 ⎠⎞ ∼⎝⎛ 100 −2−58 10−1 ∣∣∣∣∣∣ 11−3 010 0−11 ⎠⎞ .
Умножим строку №2 на −51 :
⎝⎛ 100 −2−58 10−1 ∣∣∣∣∣∣ 11−3 010 0−11 ⎠⎞ ∼⎝⎛ 100 −218 10−1 ∣∣∣∣∣∣ 1−51 −3 0−51 0 051 1 ⎠⎞ .
Прибавим к строке №3 строку №2, умноженную на -8:
⎝⎛ 100 −218 10−1 ∣∣∣∣∣∣ 1−51 −3 0−51 0 051 1 ⎠⎞ ∼⎝⎛ 100 −210 10−1 ∣∣∣∣∣∣ 1−51 −57 0−51 58 051 −53 ⎠⎞ .
Умножим строку №3 на -1:
⎝⎛ 100 −210 10−1 ∣∣∣∣∣∣ 1−51 −57 0−51 58 051 −53 ⎠⎞ ∼⎝⎛ 100 −210 101 ∣∣∣∣∣∣ 1−51 57 0−51 −58 051 53 ⎠⎞ .
Прибавим к строке №1 строку №3, умноженную на -1:
⎝⎛ 100 −210 101 ∣∣∣∣∣∣ 1−51 57 0−51 −58 051 53 ⎠⎞ ∼⎝⎛ 100 −210 001 ∣∣∣∣∣∣ −52 −51 57 58 −51 −58 −53 51 53 ⎠⎞ .
Прибавим к строке №1 строку №2, умноженную на 2:
⎝⎛ 100 −210 001 ∣∣∣∣∣∣ −52 −51 57 58 −51 −58 −53 51 53 ⎠⎞ ∼⎝⎛ 100 010 001 ∣∣∣∣∣∣ −54 −51 57 56 −51 −58 −51 51 53 ⎠⎞ .
A−1=⎝⎛ −54 −51 57 56 −51 −58 −51 51 53 ⎠⎞ =51 ⎝⎛ −4−17 6−1−8 −113 ⎠⎞ .
Подставим матрицы в равенство X=A−1⋅B:
⎝⎛ x1 x2 x3 ⎠⎞ =51 ⎝⎛ −4−17 6−1−8 −113 ⎠⎞ ⋅⎝⎛ 12−2 ⎠⎞ =51 ⎝⎛ 10−5−15 ⎠⎞ =⎝⎛ 2−1−3 ⎠⎞ .
Получили равенство ⎝⎛ x1 x2 x3 ⎠⎞ =⎝⎛ 2−1−3 ⎠⎞ . Исходя из этого, имеем: x1 =2,x2 =−1,x3 =−3.
Ответ: x1 =2,x2 =−1,x3 =−3.
Пример 2
Решить систему ⎩⎪⎨⎪⎧ 3x1 +2x2 +x3 =5,2x1 +3x2 +x3 =1,2x1 +x2 +3x3 =11. с помощью обратной матрицы.
Запишем систему в матричной форме A⋅X=B,
где A=⎝⎛ 322 231 113 ⎠⎞ ,
X=⎝⎛ x1 x2 x3 ⎠⎞ ,
B=⎝⎛ 5111 ⎠⎞ :
⎝⎛ 322 231 113 ⎠⎞ ⋅⎝⎛ x1 x2 x3 ⎠⎞ =⎝⎛ 5111 ⎠⎞ .
∣∣∣∣∣∣ 322 231 113 ∣∣∣∣∣∣ =12 =0, значит, уравнение можно решить методом обратной матрицы.
Найдем обратную матрицу A−1 по формуле A−1=∣A∣1 ⋅A∗T , где A∗T — транспонированная матрица алгебраических дополнений.
A∗T =⎝⎛ a11 a12 a13 a21 a22 a23 a31 a32 a33 ⎠⎞ , aij — алгебраические дополнения матрицы A.
A∗T =⎝⎛ 8−4−4 −571 −1−15 ⎠⎞ .
A−1=121 ⋅⎝⎛ 8−4−4 −571 −1−15 ⎠⎞ .
Подставим матрицы в равенство X=A−1⋅B:
⎝⎛ x1 x2 x3 ⎠⎞ =121 ⎝⎛ 8−4−4 −571 −1−15 ⎠⎞ ⋅⎝⎛ 5111 ⎠⎞ =121 ⎝⎛ 24−2436 ⎠⎞ =⎝⎛ 2−23 ⎠⎞ .
Получили равенство ⎝⎛ x1 x2 x3 ⎠⎞ =⎝⎛ 2−23 ⎠⎞ .
Исходя из этого, имеем: x1 =2,x2 =−2,x3 =3.
Ответ: x1 =2,x2 =−2,x3 =3.
На Студворк вы можете заказать статью по математике онлайн у профильных экспертов!
Тест по теме “Линейные уравнения и и метод обратной матрицы”




Комментарии