Нами были рассмотрены действия сложения, вычитания и умножения матриц на число. Еще одним действием над ними является умножение. Выполняется оно сложнее, а само правило может показаться немного странным. При его выполнении важно уметь определять размер матриц. Это понятие было рассмотрено в теме «Что такое матрица».
Онлайн-калькулятор
Как умножать матрицы
Приступим к рассмотрению умножения матриц.
Нам известно, что складывать и вычитать можно матрицы, которые имеют одинаковый размер. С умножением дела обстоят немного сложнее.
Какие матрицы можно умножать
Матрицу P можно умножить на матрицу K только в том случае, если число столбцов матрицы P равняется числу строк матрицы K. Матрицы, для которых данное условие не выполняется, умножать нельзя.
Пример 1
Определим, можно ли умножить матрицу
K=(1518 2710 ) на матрицу L=(3516 ).
Матрица K состоит из 2 строк и 2 столбцов, а матрица L — из 2 строк и 1 столбца. Число столбцов матрицы K равно числу строк матрицы L, значит, матрицу K можно умножить на матрицу L.
Пример 2
Переставим матрицы местами и определим, можно ли умножить матрицу
F=(3516 ) на матрицу C=(1518 2710 ).
Матрица F состоит из 2 строк и 1 столбца, а матрица C — из 2 строк и 2 столбцов. Число столбцов матрицы F не равно числу строк матрицы C, значит, матрицу F нельзя умножить на матрицу C.
Произведение матрицы A размера m×n и матрицы B размера n×k — это матрица C размера m×k, в которой элемент cij равен сумме произведений элементов i строки матрицы A на соответствующие элементы j столбца матрицы B:cij =ai1 b1j +ai2 b2j +...+ain bnj .
Умножение матриц осуществляется путем умножения строки на столбец. Находятся произведения первого элемента строки и первого элемента столбца, второго элемента строки и второго элемента столбца и т.д. Затем полученные произведения суммируются.
Алгоритм нахождения произведения матриц
- определить размеры матриц;
- если число столбцов первой матрицы совпадает с числом строк второй матрицы, то выполнять умножение.
Рассмотрим пример умножения матрицы
A=⎝⎜⎜⎛ a11 a21 a31 a41 a12 a22 a32 a42 ⎠⎟⎟⎞
на матрицу
B=(b11 b21 b12 b22 b13 b23 ).
Матрица A состоит из 4 строк и 2 столбцов, а матрица B — из 2 строк и 3 столбцов. Число столбцов матрицы A равно числу строк матрицы B, значит, можно найти произведение C=A⋅B. Причем матрица C будет иметь размер 4×3. Найдем элементы c12 (выделен красными стрелками) и c33 (выделен синими стрелками):
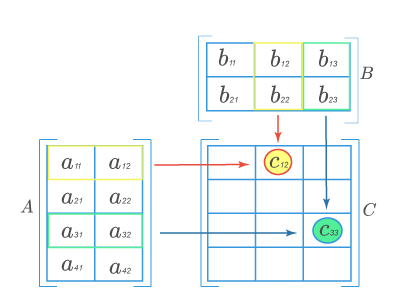
Для того чтобы найти элемент c12 нужно перемножать соответствующие элементы 1 строки матрицы A и 2 столбца матрицы B:c12 =a11 ⋅b12 +a12 ⋅b22 . Для того чтобы найти элемент c33 нужно перемножать соответствующие элементы 3 строки матрицы A и 3 столбца матрицы B: c33 =a31 ⋅b13 +a32 ⋅b23 . Так находят все элементы.
Таким образом, матрица C может быть найдена следующим образом:
A⋅B=⎝⎜⎜⎛ a11 a21 a31 a41 a12 a22 a32 a42 ⎠⎟⎟⎞ ⋅(b11 b21 b12 b22 b13 b23 )=
=⎝⎜⎜⎛ a11 ⋅b11 +a12 ⋅b21 a21 ⋅b11 +a22 ⋅b21 a31 ⋅b11 +a32 ⋅b21 a41 ⋅b11 +a42 ⋅b21 a11 ⋅b12 +a12 ⋅b22 a21 ⋅b12 +a22 ⋅b22 a31 ⋅b12 +a32 ⋅b22 a41 ⋅b12 +a42 ⋅b22 a11 ⋅b13 +a12 ⋅b23 a21 ⋅b13 +a22 ⋅b23 a31 ⋅b13 +a32 ⋅b23 a41 ⋅b13 +a42 ⋅b23 ⎠⎟⎟⎞
Произведение B⋅A нельзя найти, поскольку число столбцов матрицы B неравно числу строк матрицы A.
Найти произведение матрицы C=(1518 2710 ) на матрицу F=(3516 ).
Матрица C имеет размер 2×2, матрица F имеет размер 2×1, значит, размер матрицы произведения будет 2×1.
C⋅F=(1518 2710 )⋅(3516 )=(15⋅35+27⋅1618⋅35+10⋅16 )=(957790 ).
Как отмечалось выше, произведение матриц F⋅C невозможно.
Найти произведение матриц K⋅L и L⋅K, если K=(1213 1714 ) на матрицу L=(1812 1110 ).
Матрица K имеет размер 2×2, матрица L имеет размер 2×2, значит, размер матрицы произведения будет 2×2.
K⋅L=(1213 1714 )⋅(1812 1110 )=(12⋅18+17⋅1213⋅18+14⋅12 12⋅11+17⋅1013⋅11+14⋅10 )=(420402 302283 )
Произведение L⋅K существует и его размер — 2×2.
L⋅K=(1812 1110 )⋅(1213 1714 )=(18⋅12+11⋅1312⋅12+10⋅13 18⋅17+11⋅1412⋅17+10⋅14 )=(359274 460344 )
Произведение двух матриц в общем случае зависит от порядка сомножителей, т.е. оно некоммутативно: A⋅B =B⋅A.
Так, для матриц K=(1213 1714 ) и L=(1812 1110 ) из рассмотренного примера K⋅L =L⋅K.
Перестановочные матрицы
Перестановочные, или коммутирующие, матрицы – матрицы, для которых выполняется равенство A⋅B=B⋅A. Они обязательно квадратные.
Проверить, являются ли перестановочными матрицы C и D, если C=(24 32 ), D=(34 33 ).
Найдем произведения этих матриц C⋅D и D⋅C.
C⋅D=(24 32 )⋅(34 33 )=(2⋅3+3⋅44⋅3+2⋅4 2⋅3+3⋅34⋅3+2⋅3 )=(1820 1518 ),
D⋅C=(34 33 )⋅(24 32 )=(3⋅2+3⋅44⋅2+3⋅4 3⋅3+3⋅24⋅3+3⋅2 )=(1820 1518 ).
Таким образом, для заданных матриц выполняется равенство C⋅D и D⋅C, поэтому они являются перестановочными.
Проверить, являются ли перестановочными матрицы F и H, если F=(32 41 ), H=(09 53 ).
Найдем произведения этих матриц F⋅H и H⋅F.
F⋅H=(32 41 )⋅(09 53 )=(3⋅0+4⋅92⋅0+1⋅9 3⋅5+4⋅32⋅5+1⋅3 )=(369 2713 ),
H⋅F=(09 53 )⋅(32 41 )=(0⋅3+5⋅29⋅3+3⋅2 0⋅4+5⋅19⋅4+3⋅1 )=(1033 539 ).
Таким образом, для заданных матриц не выполняется равенство F⋅H и H⋅F, поэтому они не являются перестановочными.




Комментарии