Примеры решения систем методом Крамера

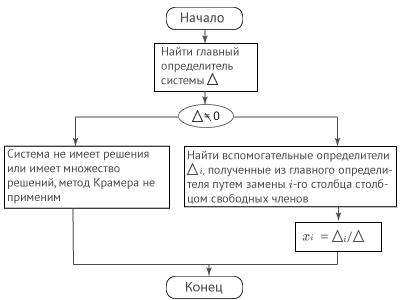
Алгоритм метода Крамера

Метод Крамера применяется для решения систем, состоящих из $n$-линейных уравнений с $n$ неизвестными.

Решение системы 2х2

Пусть дана система, состоящая из двух уравнений с двумя неизвестными

$\begin{cases} 45x+74y=1949\\ 34x+69y=1682 \end{cases}$

Решение

Вычислим главный определитель системы

$\Delta = \begin{vmatrix} 45 & 74 \\ 34 & 69 \\ \end{vmatrix} =45*69-74*34=589$

Главный определитель системы $\Delta\neq0$, значит, по правилу Крамера система имеет единственное решение.

Вспомогательные определители:

$\Delta_1 = \begin{vmatrix} 1949 & 74 \\ 1682 & 69 \\ \end{vmatrix} =1949*69-74*1682=10013$

$\Delta_2 = \begin{vmatrix} 45 & 1949 \\ 34 & 1682 \\ \end{vmatrix} =45*1682-1949*34=9424$

По формулам Крамера получаем

$x=\frac{10013}{589}=17$

$y=\frac{9424}{589}=16$

Ответ: $x=1$, $y=2$.

Решение системы 3х3

Пусть дана система, состоящая из трех уравнений с тремя неизвестными

$\begin{cases} 75x_1-27x_239x_3=954 \\41x_1+48x_2-97x_3=576 \\22x_1+67x_2+37x_3=4515 \end{cases}$

Решение
Вычислим главный определитель системы

$\Delta = \begin{vmatrix} 75 & -27 & 39\\ 41 & 48 & -97\\ 22 & 67 & 37\\ \end{vmatrix} =75*(48*37-67*(-97))+27*(41*37-22*(-97))+39*(41*67-22*48)=785151$

Главный определитель системы $\Delta\neq0$, значит, по правилу Крамера система имеет единственное решение.

$\Delta_1 = \begin{vmatrix} 954 & -27 & 39\\ 576 & 48 & -97\\ 4515 & 67 & 37\\ \end{vmatrix} =954*(48*37-67*(-97))+27*(576*37-4515*(-97))+39*(576*67-4515*48)=13347567$

$\Delta_2 = \begin{vmatrix} 75 & 957 & 39\\ 41 & 576 & -97\\ 22 & 4515 & 37\\ \end{vmatrix} =75*(576*37-4515*(-97))-954*(41*37-22*(-97))+39*(41*4515-22*576)=37687248$

$\Delta_3 = \begin{vmatrix} 75 & -27 & 954\\ 41 & 48 & 576\\ 22 & 67 & 4515\\ \end{vmatrix} =75*(48*4515-67*576)+27*(41*4515-22*576)+954*(41*67-22*48)=19628775$

По формулам Крамера получаем

$x_1=\frac{13347567}{785151}=17$

$x_2=\frac{37687248}{785151}=48$

$x_3=\frac{19628775}{785151}=25$

Ответ: $x_1=17$, $x_2=48$, $x_3=25$.

Возникли трудности с работой по этой теме? У нас вы можете заказать научную статью по математике по низкой цене!

Тест по теме «Примеры решения систем методом Крамера»