Производная неявной функции

Производная неявной функции $y(x)$ , заданной уравнением $F(x,y)=0$ вычисляется по формуле

$\frac{dy}{dx}=-\frac{F'_x(x,y)}{F'_y(x,y)},$

где

$F'_x=\frac{\partial F}{\partial x}$ , $F'_y=\frac{\partial F}{\partial y}$ – частные производные.

Пример 1

Найти производную функции $y(x)$ , заданной неявно $x^2e^y+y=1$ и ее экстремумы.

Имеем $F(x,y)=x^2e^y+y-1$ . Частные производные

$\frac{\partial F}{\partial x}=\frac{\partial}{\partial x}\left(x^2e^y+y-1\right)=2xe^y,\quad \frac{\partial F}{\partial y}=\frac{\partial}{\partial y}\left(x^2e^y+y-1\right)=x^2e^y+1.$

Производная неявной функции

$\frac{dy}{dx}=-\frac{F'_x(x,y)}{F'_y(x,y)}=-\frac{2xe^y}{x^2e^y+1}.$

Учитывая, что из определения неявной функции $x^2e^y+y=1$ следует, что $xe^y=(1-y)/x$ , получим

$\frac{dy}{dx}=-\frac{2xe^y}{x^2e^y+1}=-\frac{2(1-y)/x}{(1-y)+1}=\frac{2(y-1)}{x(2-y)}.$

Отсюда следует, что точка экстремума функции имеет ординату $y=1$ на графике. Подстановка $y=1$ в определяющее функцию равенство $x^2e^y+y=1$ дает $x^2+1=1$ , то есть $x=0$ . Следовательно, неявная функция $y(x)$ имеет экстремум в точке $x=0$ и его значение равно $y(0)=1$ .

Вторая производная неявной функции $y(x)$ , заданной уравнением $F(x,y)=0$ вычисляется по формуле

$\frac{d^2y}{dx^2}=-\frac{F_{xx}''F_y'^2-2F_{xy}''F_x'F_y'+F_{yy}''F_x'^2}{F_y'^3},$

где

$F''_{\alpha\beta}=\frac{\partial^2 F}{\partial \alpha\partial\beta}$ – вторые частные производные.

Пример 2

Найти вторую производную функции $y(x)$ , заданной неявно $x^2e^y+y=1$ и точки перегиба ее графика.

Имеем $F(x,y)=x^2e^y+y-1$ . Первые частные производные вычислены выше. Вторые частные производные:

$\frac{\partial^2 F}{\partial x^2}=\frac{\partial}{\partial x}\left(2xe^y\right)=2e^y,$

$\frac{\partial^2 F}{\partial y\partial x}=\frac{\partial}{\partial y}\left(2xe^y\right)=2xe^y,$

$\frac{\partial^2 F}{\partial y^2}=\frac{\partial}{\partial y}\left(x^2e^y+1\right)=x^2e^y.$

Вторая производная неявной функции

$\frac{d^2y}{dx^2}=-\frac{2e^y\left(x^2e^y+1\right)^2-2\cdot 2xe^y\cdot 2xe^y\left(x^2e^y+1\right)+x^2e^y\left(2xe^y\right)^2)}{\left(x^2e^y+1\right)^3}.$

Учитывая, что из определения неявной функции $x^2e^y+y=1$ следует, что $xe^y=(1-y)/x$ , получим

$\frac{d^2y}{dx^2}=-\frac{2e^y(2-y)^2-8e^y(1-y)(2-y)+4e^y(1-y)^2)}{(2-y)^3}=\frac{2e^y\left(y^2-4y+2\right)}{(2-y)^3}.$

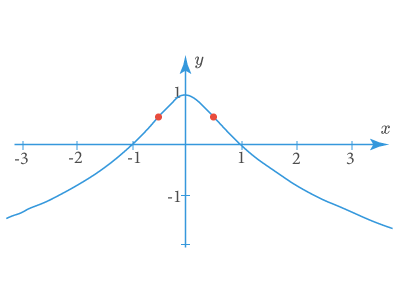
Ординаты точек перегиба на графике найдем из уравнения $y''=0$ , то есть $y^2-4y+2=0$ . Решениями данного уравнения являтся числа $2\pm\sqrt{2}$ . Однако, из равенства $y=1-x^2e^y$ следует, что $y\le 1$ . Таким образом, точки перегиба имеют ординату $y_0=2-\sqrt{2}$ и абсциссы