Общее уравнение прямой на плоскости
«Школьное» уравнение прямой не является уравнением прямой общего вида, так как не может задать вертикальные прямые, как, например, прямую , параллельную оси ординат.
Общим уравнением прямой на плоскости называется уравнение вида
.
Вектор на плоскости с декартовыми координатами и является вектором нормали прямой , то есть перпендикулярен данной прямой.
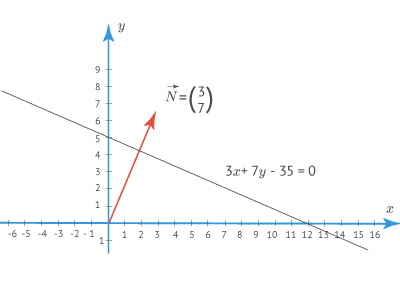
Пример 1
Общее уравнение прямой, проходящей через точку , перпендикулярно вектору получается из уравнения
то есть имеет вид
Уравнение прямой в отрезках
Пусть прямая пересекает обе координатных оси, причем в разных точках. Это равносильно тому, что все три числа и ненулевые. В этом случае уравнение можно записать как
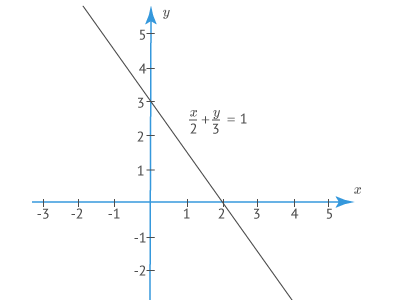
Уравнением прямой в отрезках называется уравнение вида
Точка пересечения данной прямой с осью имеет абсциссу, равную . Тогда как точка пересечения с осью имеет ординату .
Нормальное уравнение прямой
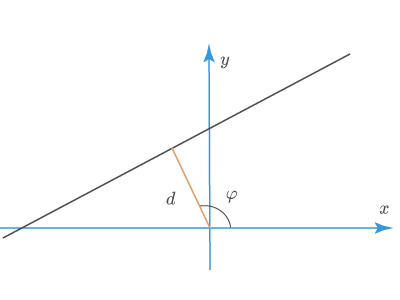
Нормальным уравнением прямой называется уравнение вида
Здесь – расстояние от прямой до начала координат, а угол определяется наклоном вектора нормали данной прямой.
Каноническое уравнение прямой
Каноническим уравнением прямой на плоскости называется уравнение вида
Здесь – координаты произвольной точки на прямой, а – координаты направляющего вектора прямой, то есть вектора, параллельного прямой.
В случае, когда (соответственно, ) прямая параллельна оси ординат и имеет вид (соответственно, параллельна оси абсцисс, ).
Уравнение прямой, проходящей через две заданные точки и удобно записывать в каноническом виде. При этом – координаты любой из точек, а – координаты вектора .
Пример 2
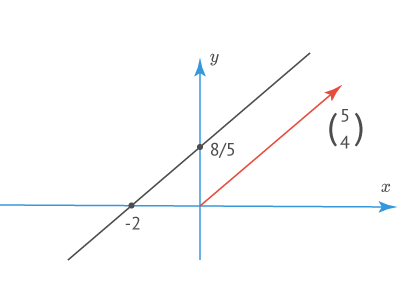
Уравнение прямой, проходящей через точки и имеет каноническую запись
то есть
Последнее уравнение может быть приведено к общему виду
или записано как уравнение в отрезках
На рисунке направляющий вектор изображен красным цветом.
Научная статья по математике на заказ от проверенных экспертов по низкой цене!



Комментарии