Тангенсом угла в прямоугольном треугольнике называют отношение противолежащего катета к прилежащему.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: тангенс угла — это отношение дальнего от рассматриваемого угла катета к ближнему катету.
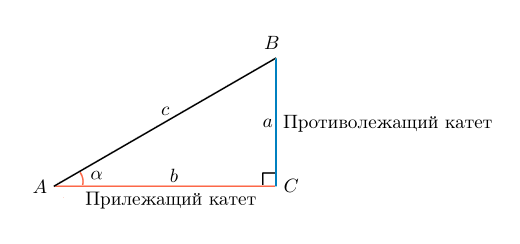
В случае с рисунком, описанным выше:
Тангенс можно найти напрямую пользуясь данной формулой, а можно и через тригонометрические тождества. Разберем подробнее задачи.
В прямоугольном треугольнике катеты равны и . Найдите тангенс угла, близлежащего к меньшей стороне.
Решение
Ответ
Формулу:
Можно записать в следующем виде:
Проверим истинность данного выражения. Подставим вместо синуса и косинуса их определения:
Получили первичное равенство, значит выражение для тангенса через отношение синуса к косинусу верно.
Решим задачу, пользуясь этой формулой.
По условию задачи известен косинус угла, равный и синус того же угла, равный . Найдите тангенс данного угла.
Решение
Ответ
Еще одно тождество помогает решить задачи, связанные с тангенсом:
Оно появляется путем деление каждого слагаемого основного тождества тригонометрии на квадрат косинуса.
Известен квадрат косинуса угла в прямоугольном треугольнике, равный . Нужно найти тангенс этого угла.
Решение
Ответ
Заказать статью по математике у экспертов биржи Студворк!




Комментарии