Найти экстремали функционала
J [ y ] = ∫ x 0 x 1 L ( x , y , y ′ ) d x
J[y]=\int\limits_{x_0}^{x_1}L\left(x,y,y'\right)\,dx
J [ y ] = x 0 ∫ x 1 L ( x , y , y ′ ) d x
при условиях
∫ x 0 x 1 G ( x , y , y ′ ) d x = C , y ( x 0 ) = y 0 , y ( x 1 ) = y 1
\int\limits_{x_0}^{x_1}G\left(x,y,y'\right)\, dx =C,\quad y(x_0)=y_0,\,\,y(x_1)=y_1
x 0 ∫ x 1 G ( x , y , y ′ ) d x = C , y ( x 0 ) = y 0 , y ( x 1 ) = y 1
У функционала J J J y ( x ) y(x) y ( x ) ∫ x 0 x 1 G ( x , y , y ′ ) d x = C , \int_{x_0}^{x_1}G\left(x,y,y'\right)\, dx =C, ∫ x 0 x 1 G ( x , y , y ′ ) d x = C ,
Рассмотрим функцию
Φ ( x , y , y ′ ; λ ) = L ( x , y , y ′ ) + λ G ( x , y , y ′ ) ,
\Phi\left(x,y,y';\lambda\right)=L\left(x,y,y'\right)+\lambda G\left(x,y,y'\right),
Φ ( x , y , y ′ ; λ ) = L ( x , y , y ′ ) + λ G ( x , y , y ′ ) ,
где λ \lambda λ
Вычисляем производные:
∂ ∂ y Φ ( x , y , y ′ ; λ ) , ∂ ∂ y ′ Φ ( x , y , y ′ ; λ ) , d d x ∂ ∂ y ′ Φ ( x , y , y ′ ; λ ) .
\frac{\partial}{\partial y}\Phi\left(x,y,y';\lambda\right),\quad\frac{\partial}{\partial y'}\Phi\left(x,y,y';\lambda\right),\quad\frac{d}{dx}\frac{\partial}{\partial y'}\Phi\left(x,y,y';\lambda\right).
∂ y ∂ Φ ( x , y , y ′ ; λ ) , ∂ y ′ ∂ Φ ( x , y , y ′ ; λ ) , d x d ∂ y ′ ∂ Φ ( x , y , y ′ ; λ ) .
Выписываем уравнение Эйлера-Лагранжа
d d x ∂ ∂ y ′ Φ ( x , y , y ′ ; λ ) = ∂ ∂ y Φ ( x , y , y ′ ; λ )
\frac{d}{dx}\frac{\partial}{\partial y'}\Phi\left(x,y,y';\lambda\right)=\frac{\partial}{\partial y}\Phi\left(x,y,y';\lambda\right)
d x d ∂ y ′ ∂ Φ ( x , y , y ′ ; λ ) = ∂ y ∂ Φ ( x , y , y ′ ; λ )
и приводим его к максимально простому виду.
Решаем полученное дифференциальное уравнение второго порядка. Выписываем общее решение
y = y ( x , C 1 , C 2 ; λ ) .
y=y\left(x,C_1,C_2;\lambda\right).
y = y ( x , C 1 , C 2 ; λ ) .
Используя граничные условия, получаем систему для определения постоянных
{ y ( x 0 , C 1 , C 2 ; λ ) = y 0 y ( x 1 , C 1 , C 2 ; λ ) = y 1
\left\{\begin{array}{l}
y\left(x_0,C_1,C_2;\lambda\right)=y_0\\
y\left(x_1,C_1,C_2;\lambda\right)=y_1
\end{array}\right.
{ y ( x 0 , C 1 , C 2 ; λ ) = y 0 y ( x 1 , C 1 , C 2 ; λ ) = y 1
Решая данную систему, получаем выражение постоянных через λ \lambda λ
C 1 = C 1 ( x 0 , x 1 , y 0 , y 1 ; λ ) , C 2 = C 2 ( x 0 , x 1 , y 0 , y 1 ; λ ) .
C_1=C_1(x_0,x_1,y_0,y_1;\lambda),\quad C_2=C_2(x_0,x_1,y_0,y_1;\lambda).
C 1 = C 1 ( x 0 , x 1 , y 0 , y 1 ; λ ) , C 2 = C 2 ( x 0 , x 1 , y 0 , y 1 ; λ ) .
Подставляем найденные в предыдущем пункте значения констант в общее решение
y ∗ ( x ; λ ) = y ( x , C 1 ( x 0 , x 1 , y 0 , y 1 ; λ ) , C 2 ( x 0 , x 1 , y 0 , y 1 ) ; λ )
y_*(x;\lambda)=y\Bigl(x,C_1(x_0,x_1,y_0,y_1;\lambda),C_2(x_0,x_1,y_0,y_1);\lambda\Bigr)
y ∗ ( x ; λ ) = y ( x , C 1 ( x 0 , x 1 , y 0 , y 1 ; λ ) , C 2 ( x 0 , x 1 , y 0 , y 1 ) ; λ )
и интегрируем:
∫ x 0 x 1 G ( x , y ∗ ( x ; λ ) , y ∗ ′ ( x ; λ ) ) d x = C ( λ ) .
\int\limits_{x_0}^{x_1}G\Bigl(x,y_*(x;\lambda),y'_*(x;\lambda)\Bigr)\,\, dx=C(\lambda).
x 0 ∫ x 1 G ( x , y ∗ ( x ; λ ) , y ∗ ′ ( x ; λ ) ) d x = C ( λ ) .
Находим значение λ \lambda λ C ( λ ) = C C(\lambda) = C C ( λ ) = C
Выписываем уравнение экстремали, подставляя в общее решение y ( x , C 1 , C 2 ; λ ) y(x,C_1,C_2;\lambda) y ( x , C 1 , C 2 ; λ )
Если подинтегральные функции L ( x , y , y ′ ) L\left(x,y,y'\right) L ( x , y , y ′ ) G ( x , y , y ′ ) G\left(x,y,y'\right) G ( x , y , y ′ )
y ′ ∂ Φ ( y , y ′ ; λ ) ∂ y ′ − Φ ( y , y ′ ; λ ) = C 1 .
y'\frac{\partial \Phi\left(y,y';\lambda\right)}{\partial y'}-\Phi\left(y,y';\lambda\right)=C_1.
y ′ ∂ y ′ ∂ Φ ( y , y ′ ; λ ) − Φ ( y , y ′ ; λ ) = C 1 .
Данное выражение определяет дифференциальное уравнение первого порядка, общее решение которого (зависящее от некоторой постоянной C 2 C_2 C 2
На практике можно выбирать – решать исходное уравнение Эйлера-Лагранжа, или воспользоваться первым интегралом.
Найти экстремали функционала
J [ y ] = ∫ 0 1 y ′ 2 d x
J[y]=\int\limits_{0}^{1}y'^2\,dx
J [ y ] = 0 ∫ 1 y ′ 2 d x
при условиях
∫ 0 1 x y d x = 1 4 , y ( 0 ) = 0 , y ( 1 ) = 1 12 .
\int\limits_{0}^{1}xy\, dx =\frac{1}{4},\quad y(0)=0,\,\,y(1)=\frac{1}{12}.
0 ∫ 1 x y d x = 4 1 , y ( 0 ) = 0 , y ( 1 ) = 1 2 1 .
Рассмотрим функцию
Φ ( x , y , y ′ ; λ ) = y ′ 2 + λ x y ,
\Phi\left(x,y,y';\lambda\right)=y'^2+\lambda xy,
Φ ( x , y , y ′ ; λ ) = y ′ 2 + λ x y ,
где λ \lambda λ
Вычисляем производные:
∂ ∂ y ( y ′ 2 + λ x y ) = λ x , ∂ ∂ y ′ ( y ′ 2 + λ x y ) = 2 y ′ ,
\frac{\partial}{\partial y}\left(y'^2+\lambda xy\right)=\lambda x,\quad\frac{\partial}{\partial y'}\left(y'^2+\lambda xy\right)=2y', ∂ y ∂ ( y ′ 2 + λ x y ) = λ x , ∂ y ′ ∂ ( y ′ 2 + λ x y ) = 2 y ′ ,
d d x ∂ ∂ y ′ ( y ′ 2 + λ x y ) = d d x 2 y ′ = 2 y ′ ′ . \frac{d}{dx}\frac{\partial}{\partial y'}\left(y'^2+\lambda xy\right)=\frac{d}{dx}2y'=2y''.
d x d ∂ y ′ ∂ ( y ′ 2 + λ x y ) = d x d 2 y ′ = 2 y ′ ′ .
Уравнение Эйлера-Лагранжа
2 y ′ ′ = λ x .
2y''=\lambda x.
2 y ′ ′ = λ x .
Полученное уравнение легко интегрируется:
y ′ ′ = λ x 2 ⇒ y ′ = λ x 2 4 + C 1 ⇒ y ( x , C 1 , C 2 ; λ ) = λ x 3 12 + C 1 x + C 2 .
y''=\frac{\lambda x}{2}\quad\Rightarrow\quad y'=\frac{\lambda x^2}{4}+C_1\quad\Rightarrow\quad y(x,C_1, C_2;\lambda)=\frac{\lambda x^3}{12}+C_1x+C_2.
y ′ ′ = 2 λ x ⇒ y ′ = 4 λ x 2 + C 1 ⇒ y ( x , C 1 , C 2 ; λ ) = 1 2 λ x 3 + C 1 x + C 2 .
Используя граничные условия, получаем систему для определения постоянных
{ λ ⋅ 0 3 12 + C 1 ⋅ 0 + C 2 = 0 λ ⋅ 1 3 12 + C 1 ⋅ 1 + C 2 = 1 12 ⇒ { C 2 = 0 C 1 = 1 − λ 12 .
\left\{\begin{array}{l}
\frac{\lambda\cdot 0^3}{12}+C_1\cdot 0+C_2=0\\
\frac{\lambda\cdot 1^3}{12}+C_1\cdot 1+C_2=\frac{1}{12}
\end{array}\right.\quad\Rightarrow\quad\left\{\begin{array}{l}
C_2=0\\
C_1=\frac{1-\lambda}{12}
\end{array}\right..
{ 1 2 λ ⋅ 0 3 + C 1 ⋅ 0 + C 2 = 0 1 2 λ ⋅ 1 3 + C 1 ⋅ 1 + C 2 = 1 2 1 ⇒ { C 2 = 0 C 1 = 1 2 1 − λ .
Подставляем найденные в предыдущем пункте значения констант в общее решение
y ∗ ( x ; λ ) = λ x 3 12 + C 1 x + C 2 = λ x 3 12 + ( 1 − λ ) x 12
y_*(x;\lambda)=\frac{\lambda x^3}{12}+C_1x+C_2=\frac{\lambda x^3}{12}+\frac{(1-\lambda)x}{12}
y ∗ ( x ; λ ) = 1 2 λ x 3 + C 1 x + C 2 = 1 2 λ x 3 + 1 2 ( 1 − λ ) x
и интегрируем функцию x y xy x y
∫ 0 1 x y ∗ ( x ; λ ) d x = ∫ 0 1 ( λ x 4 12 + ( 1 − λ ) x 2 12 ) d x = 1 12 ( λ 5 + 1 − λ 3 ) .
\int\limits_{0}^{1}xy_*(x;\lambda)\, dx=\int\limits_{0}^{1}\left(\frac{\lambda x^4}{12}+\frac{(1-\lambda)x^2}{12}
\right)\,dx=\frac{1}{12}\left(\frac{\lambda }{5}+\frac{1-\lambda}{3}\right).
0 ∫ 1 x y ∗ ( x ; λ ) d x = 0 ∫ 1 ( 1 2 λ x 4 + 1 2 ( 1 − λ ) x 2 ) d x = 1 2 1 ( 5 λ + 3 1 − λ ) .
Найдем значение λ \lambda λ
1 12 ( λ 5 + 1 − λ 3 ) = 1 4 .
\frac{1}{12}\left(\frac{\lambda }{5}+\frac{1-\lambda}{3}\right)=\frac{1}{4}.
1 2 1 ( 5 λ + 3 1 − λ ) = 4 1 .
Получаем λ = − 20 \lambda=-20 λ = − 2 0
Выписываем уравнение экстремали, подставляя в общее решение найденные значения постоянных
y ∗ ( x ) = y ∗ ( x ; − 20 ) = − 5 x 3 3 + 7 x 4 . y_*(x)=y_*(x;-20)=-\frac{5 x^3}{3}+\frac{7x}{4}.
y ∗ ( x ) = y ∗ ( x ; − 2 0 ) = − 3 5 x 3 + 4 7 x .
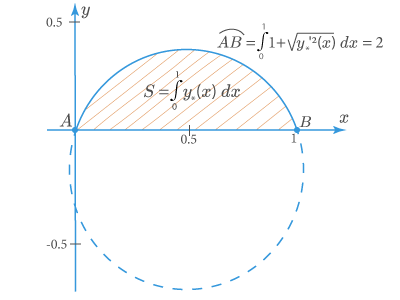
Найти экстремали функционала
J [ y ] = ∫ 0 1 y d x
J[y]=\int\limits_{0}^{1}{y}\,d x
J [ y ] = 0 ∫ 1 y d x
при условиях
∫ 0 1 1 + y ′ 2 d x = 2 , y ( 0 ) = y ( 1 ) = 0
\int\limits_{0}^{1}\sqrt{1+y'^2}\, dx =2,\quad y(0)=y(1)=0
0 ∫ 1 1 + y ′ 2 d x = 2 , y ( 0 ) = y ( 1 ) = 0
1,2. Подинтегральные функции L ( x , y , y ′ ) = y L\left(x,y,y'\right)={y} L ( x , y , y ′ ) = y G ( x , y , y ′ ) = 1 + y ′ 2 G\left(x,y,y'\right)=\sqrt{1+y'^2} G ( x , y , y ′ ) = 1 + y ′ 2 x x x
y ′ ∂ ∂ y ′ ( y + λ 1 + y ′ 2 ) − ( y + λ 1 + y ′ 2 ) = C 1 .
y'\frac{\partial }{\partial y'}\left(y+\lambda \sqrt{1+y'^2}\right)-\left(y+\lambda\sqrt{1+y'^2}\right)=C_1.
y ′ ∂ y ′ ∂ ( y + λ 1 + y ′ 2 ) − ( y + λ 1 + y ′ 2 ) = C 1 .
Вычислив частную производную и выполнив элементарные преобразования, получим уравнение
y ′ = λ 2 ( y + C 1 ) 2 − 1 .
y'=\sqrt{\frac{\lambda^2}{(y+C_1)^2}-1}.
y ′ = ( y + C 1 ) 2 λ 2 − 1 .
Отсюда следует, что
d x = ( C 1 + y ) d y λ 2 − ( C 1 + y ) 2 .
d x=\frac{(C_1+y) \,dy}{\sqrt{\lambda^2-(C_1+y)^2}}.
d x = λ 2 − ( C 1 + y ) 2 ( C 1 + y ) d y .
Интегрируя, получим
x = ∫ ( C 1 + y ) d y λ 2 − ( C 1 + y ) 2 = − 1 2 ∫ d ( λ 2 − ( C 1 + y ) 2 ) C 1 2 − y 2 = − λ 2 − ( C 1 + y ) 2 + C 2 .
x=\int\frac{(C_1+y)\,dy}{\sqrt{\lambda^2-(C_1+y)^2}}=-\frac{1}{2}\int\frac{d \left(\lambda^2-(C_1+y)^2\right)}{\sqrt{C_1^2-y^2}}=-\sqrt{\lambda^2-(C_1+y)^2}+C_2.
x = ∫ λ 2 − ( C 1 + y ) 2 ( C 1 + y ) d y = − 2 1 ∫ C 1 2 − y 2 d ( λ 2 − ( C 1 + y ) 2 ) = − λ 2 − ( C 1 + y ) 2 + C 2 .
Таким образом, общее решение уравнения Эйлера-Лагранжа
y ( x , C 1 , C 2 ; λ ) = λ 2 − ( x − C 2 ) 2 − C 1 .
y(x,C_1,C_2;\lambda)=\sqrt{\lambda^2-(x-C_2)^2}-C_1.
y ( x , C 1 , C 2 ; λ ) = λ 2 − ( x − C 2 ) 2 − C 1 .
Используя граничные условия, получаем систему для определения постоянных
{ 0 = λ 2 − ( 0 − C 2 ) 2 − C 1 0 = λ 2 − ( 1 − C 2 ) 2 − C 1 ⇔ { C 2 2 = ( 1 − C 2 ) 2 C 1 = λ 2 − C 2 2 ⇔ { C 2 = 1 2 C 1 = λ 2 − 1 4 .
\left\{\begin{array}{l}
0=\sqrt{\lambda^2-(0-C_2)^2}-C_1\\
0=\sqrt{\lambda^2-(1-C_2)^2}-C_1
\end{array}\right.\Leftrightarrow \left\{\begin{array}{l}
C_2^2=(1- C_2)^2\\
C_1=\sqrt{\lambda^2-C_2^2}\end{array}\right.
\Leftrightarrow \left\{\begin{array}{l}
C_2=\frac{1}{2}\\
C_1=\sqrt{\lambda^2-\frac{1}{4}}
\end{array}\right..
{ 0 = λ 2 − ( 0 − C 2 ) 2 − C 1 0 = λ 2 − ( 1 − C 2 ) 2 − C 1 ⇔ { C 2 2 = ( 1 − C 2 ) 2 C 1 = λ 2 − C 2 2 ⇔ { C 2 = 2 1 C 1 = λ 2 − 4 1 .
Подставляем найденные в предыдущем пункте значения констант в общее решение уравнения Эйлера-Лагранжа:
y ∗ ( x ; λ ) = λ 2 − ( x − 1 2 ) 2 − λ 2 − 1 4 .
y_*(x;\lambda)=\sqrt{\lambda^2-\left(x-\frac{1}{2}\right)^2}-\sqrt{\lambda^2-\frac{1}{4}}.
y ∗ ( x ; λ ) = λ 2 − ( x − 2 1 ) 2 − λ 2 − 4 1 .
Заметим, что для определенности выражения должно выполняться неравенство λ > 1 2 \lambda>\frac{1}{2} λ > 2 1
Вычисляем производную
y ∗ ′ ( x ; λ ) = − x − 1 2 λ 2 − ( x − 1 2 ) 2 .
y_*'(x;\lambda)=-\frac{x-\frac{1}{2}}{\sqrt{\lambda^2-\left(x-\frac{1}{2}\right)^2}}.
y ∗ ′ ( x ; λ ) = − λ 2 − ( x − 2 1 ) 2 x − 2 1 .
Интегрируем:
∫ 0 1 1 + y ∗ ′ 2 d x = λ ∫ 0 1 d x λ 2 − ( x − 1 2 ) 2 = 2 λ arcsin 1 2 λ .
\int\limits_0^1\sqrt{1+y_*'^2}\,dx=\lambda\int\limits_0^1\frac{dx}{\sqrt{\lambda^2-\left(x-\frac{1}{2}\right)^2}}=2\lambda\arcsin\frac{1}{2\lambda}.
0 ∫ 1 1 + y ∗ ′ 2 d x = λ 0 ∫ 1 λ 2 − ( x − 2 1 ) 2 d x = 2 λ arcsin 2 λ 1 .
Найдем значение λ \lambda λ
2 λ arcsin 1 2 λ = 2 ⇒ λ sin 1 λ = 1 2 .
2\lambda\arcsin\frac{1}{2\lambda}=2\quad\Rightarrow\quad\lambda\sin\frac{1}{\lambda}=\frac{1}{2}.
2 λ arcsin 2 λ 1 = 2 ⇒ λ sin λ 1 = 2 1 .
Полученное уравнение имеет единственный корень1 λ 0 \lambda_0 λ 0
1Рассмотрим функцию f ( λ ) = λ sin 1 λ f(\lambda)=\lambda\sin\frac{1}{\lambda} f ( λ ) = λ sin λ 1 f ( 1 / 2 ) < 1 / 2 f(1/2)<1/2 f ( 1 / 2 ) < 1 / 2 f ( 1 ) > 1 / 2 f(1)>1/2 f ( 1 ) > 1 / 2 f ( λ ) = 1 / 2 f(\lambda)=1/2 f ( λ ) = 1 / 2 λ > 1 2 \lambda>\frac{1}{2} λ > 2 1 f ′ ( λ ) = sin 1 λ − 1 λ cos 1 λ > 0. f'(\lambda)=\sin\frac{1}{\lambda}-\frac{1}{\lambda}\cos\frac{1}{\lambda}>0. f ′ ( λ ) = sin λ 1 − λ 1 cos λ 1 > 0 .
2В силу того, что sin 1 λ > 1 λ − 1 6 λ 3 \sin\frac{1}{\lambda}>\frac{1}{\lambda}-\frac{1}{6\lambda^3} sin λ 1 > λ 1 − 6 λ 3 1 λ 0 < 1 3 \lambda_0<\frac{1}{\sqrt{3}} λ 0 < 3 1 λ 0 ≈ 0.528. \lambda_0\approx 0.528. λ 0 ≈ 0 . 5 2 8 .
1 2 < λ 0 < 1 3 .
\frac{1}{2}<\lambda_0<\frac{1}{\sqrt{3}}.
2 1 < λ 0 < 3 1 .
Таким образом, искомая экстремаль – дуга окружности
y ∗ ( x ) = λ 0 2 − ( x − 1 2 ) 2 − λ 0 2 − 1 4 .
y_*(x)=\sqrt{\lambda_0^2-\left(x-\frac{1}{2}\right)^2}-\sqrt{\lambda_0^2-\frac{1}{4}}.
y ∗ ( x ) = λ 0 2 − ( x − 2 1 ) 2 − λ 0 2 − 4 1 .
Длина дуги A B ⌢ = ∫ 0 1 1 + y ′ 2 d x = 2 \overset\frown{AB}=\int\limits_{0}^{1}\sqrt{1+y'^2}\, dx =2 A B ⌢ = 0 ∫ 1 1 + y ′ 2 d x = 2 J [ y ∗ ] J[y_*] J [ y ∗ ]
Пример изопериметрической задачи, имеющей бесконечно много экстремалей
Найти экстремали функционала
J [ y ] = ∫ 0 1 ( y 2 + y ′ 2 ) d x
J[y]=\int\limits_{0}^{1}\left(y^2+y'^2\right)\,d x
J [ y ] = 0 ∫ 1 ( y 2 + y ′ 2 ) d x
при условиях
∫ 0 1 y 2 d x = 1 , y ( 0 ) = y ( 1 ) = 0
\int\limits_{0}^{1}y^2\, dx =1,\quad y(0)=y(1)=0
0 ∫ 1 y 2 d x = 1 , y ( 0 ) = y ( 1 ) = 0
Рассмотрим функцию
Φ ( x , y , y ′ ; λ ) = y 2 + y ′ 2 + λ y 2 = y ′ 2 + ( 1 + λ ) y 2 ,
\Phi\left(x,y,y';\lambda\right)=y^2+y'^2+\lambda y^2=y'^2+(1+\lambda)y^2,
Φ ( x , y , y ′ ; λ ) = y 2 + y ′ 2 + λ y 2 = y ′ 2 + ( 1 + λ ) y 2 ,
где λ \lambda λ
Вычисляем производные:
∂ ∂ y ( y ′ 2 + ( 1 + λ ) y 2 ) = 2 ( 1 + λ ) y , ∂ ∂ y ′ ( y ′ 2 + ( 1 + λ ) y 2 ) = 2 y ′ ,
\frac{\partial}{\partial y}\left(y'^2+(1+\lambda)y^2\right)=2(1+\lambda)y,\quad\frac{\partial}{\partial y'}\left(y'^2+(1+\lambda)y^2\right)=2y', ∂ y ∂ ( y ′ 2 + ( 1 + λ ) y 2 ) = 2 ( 1 + λ ) y , ∂ y ′ ∂ ( y ′ 2 + ( 1 + λ ) y 2 ) = 2 y ′ , d d x ∂ ∂ y ′ ( y ′ 2 + ( 1 + λ ) y 2 ) = d d x 2 y ′ = 2 y ′ ′ . \frac{d}{dx}\frac{\partial}{\partial y'}\left(y'^2+(1+\lambda)y^2\right)=\frac{d}{dx}2y'=2y''.
d x d ∂ y ′ ∂ ( y ′ 2 + ( 1 + λ ) y 2 ) = d x d 2 y ′ = 2 y ′ ′ .
Уравнение Эйлера-Лагранжа
2 y ′ ′ = 2 ( 1 + λ ) y ⇒ y ′ ′ = ( 1 + λ ) y .
2y''=2(1+\lambda)y\Rightarrow y''=(1+\lambda) y.
2 y ′ ′ = 2 ( 1 + λ ) y ⇒ y ′ ′ = ( 1 + λ ) y .
2,3. Полученное уравнение явлется ЛОДУ второго порядка.
Рассмотрим три случая.
Если 1 + λ > 0 1+\lambda>0 1 + λ > 0 y ′ ′ = ( 1 + λ ) y y''=(1+\lambda) y y ′ ′ = ( 1 + λ ) y
y = C 1 ch 1 + λ x + C 2 sh 1 + λ x .
y=C_1\operatorname{ch}\sqrt{1+\lambda}x+C_2\operatorname{sh}\sqrt{1+\lambda}x.
y = C 1 c h 1 + λ x + C 2 s h 1 + λ x .
Граничные условия приводят к тривиальному решению:
{ 0 = C 1 ch 0 + C 2 sh 0 0 = C 1 ch 1 + λ + C 2 sh 1 + λ ⇒ { C 1 = 0 C 2 sh 1 + λ = 0 ⇒ { C 1 = 0 C 2 = 0 ,
\left\{\begin{array}{l}
0=C_1\operatorname{ch} 0+C_2\operatorname{sh}0\\
0=C_1\operatorname{ch}\sqrt{1+\lambda}+C_2\operatorname{sh}\sqrt{1+\lambda}
\end{array}\right.\quad\Rightarrow\quad\left\{\begin{array}{l}
C_1=0\\
C_2\operatorname{sh}\sqrt{1+\lambda}=0
\end{array}\right.
\quad\Rightarrow\quad\left\{\begin{array}{l}
C_1=0\\
C_2=0
\end{array}\right.,
{ 0 = C 1 c h 0 + C 2 s h 0 0 = C 1 c h 1 + λ + C 2 s h 1 + λ ⇒ { C 1 = 0 C 2 s h 1 + λ = 0 ⇒ { C 1 = 0 C 2 = 0 ,
которое не может быть искомой экстремалью в силу изопериметрического условия.
Если 1 + λ = 0 1+\lambda=0 1 + λ = 0 y ′ ′ = 0 y''=0 y ′ ′ = 0 y = C 1 x + C 2 .
y=C_1x+C_2.
y = C 1 x + C 2 .
Граничные условия также приводят к тривиальному решению.
Если 1 + λ < 0 1+\lambda<0 1 + λ < 0 y ′ ′ = ( 1 + λ ) y y''=(1+\lambda) y y ′ ′ = ( 1 + λ ) y
y = C 1 cos − 1 − λ x + C 2 sin − 1 − λ x .
y=C_1\cos\sqrt{-1-\lambda}x+C_2\sin\sqrt{-1-\lambda}x.
y = C 1 cos − 1 − λ x + C 2 sin − 1 − λ x .
Граничные условия приводят к соотношению
{ 0 = C 1 cos 0 + C 2 sin 0 0 = C 1 cos − 1 − λ + C 2 sin − 1 − λ ⇒ { C 1 = 0 C 2 sin − 1 − λ = 0
\left\{\begin{array}{l}
0=C_1\cos 0+C_2\sin 0\\
0=C_1\cos\sqrt{-1-\lambda}+C_2\sin\sqrt{-1-\lambda}
\end{array}\right.\quad\Rightarrow\quad\left\{\begin{array}{l}
C_1=0\\
C_2\sin\sqrt{-1-\lambda}=0
\end{array}\right.
{ 0 = C 1 cos 0 + C 2 sin 0 0 = C 1 cos − 1 − λ + C 2 sin − 1 − λ ⇒ { C 1 = 0 C 2 sin − 1 − λ = 0
Таким образом, C 2 C_2 C 2 λ \lambda λ λ n = − 1 − π 2 n 2 \lambda_n=-1-\pi^2n^2 λ n = − 1 − π 2 n 2 n n n
Подставляем найденные в предыдущем пункте значения констант в общее решение
y n ( x ) = C 2 sin π n x .
y_n(x)=C_2\sin{\pi n x}.
y n ( x ) = C 2 sin π n x .
Интегрируем
∫ 0 1 y n 2 d x = C 2 2 ∫ 0 1 sin 2 π n x d x = C 2 2 2 .
\int\limits_{0}^{1}y_n^2\, dx =C_2^2\int\limits_{0}^{1}\sin^2\pi n x\, dx =\frac{C_2^2}{2}.
0 ∫ 1 y n 2 d x = C 2 2 0 ∫ 1 sin 2 π n x d x = 2 C 2 2 .
Найдем значение C 2 C_2 C 2
C 2 2 2 = 1 ⇒ C 2 = ± 2
\frac{C_2^2}{2}=1\quad\Rightarrow\quad C_2=\pm\sqrt{2}
2 C 2 2 = 1 ⇒ C 2 = ± 2
Выписываем уравнение экстремалей, подставляя в общее решение найденные значения постоянных
y n ( x ) = 2 sin π n x .
y_n(x)=\sqrt{2}\sin\pi n x.
y n ( x ) = 2 sin π n x .
Здесь n n n
Не получается самостоятельно разобраться с темой? Заказать написание статьи по математике !



Комментарии