Ряды Фурье – способ представления сложной функции суммой более простых, хорошо известных.
Синус и косинус – это периодические функции. Еще они образуют ортогональный базис. Это свойство можно объяснить по аналогии с осями и на координатной плоскости. Точно так же, как мы можем описать координаты точки относительно осей, мы можем описать любую функцию относительно синусов и косинусов. Тригонометрические функции хорошо изучены и их легко применять в математике.
Представить синусы и косинусы можно в виде таких волн:
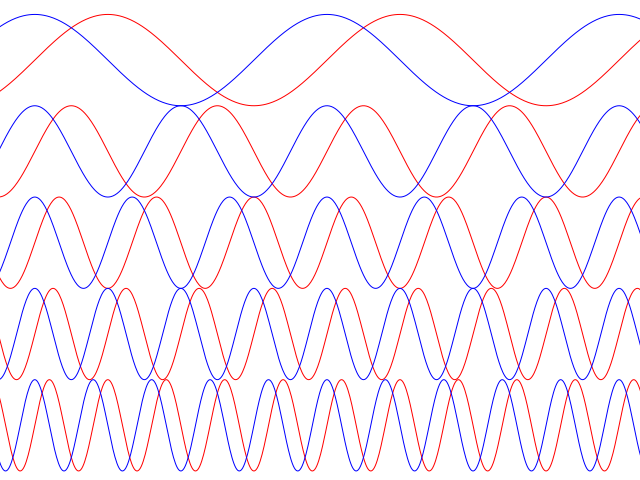
Синие – это косинусы, красные – синусы. Еще такие волны называют гармониками. Косинусы – четными, синусы – нечетными. Термин гармоника пришел еще из античности и связан с наблюдениями о взаимосвязи высот звуков в музыке.
Что такое ряд Фурье
Такой ряд, где в качестве простейших используются функции синуса и косинуса, называется тригонометрическим. Назван он в честь своего изобретателя Жана Батиста Жозефа Фурье, в конце XVIII–начале XIX в. доказавшего, что любую функцию можно представить в виде комбинации таких гармоник. И чем больше их взять, тем точнее это представление будет. Для примера картинка ниже: можно заметить, что с большим количеством гармоник, т. е. членов ряда Фурье, красный график становится все ближе к синему – исходной функции.
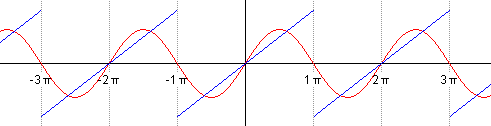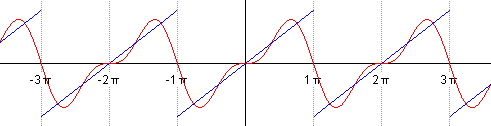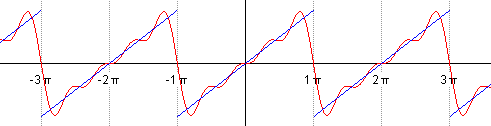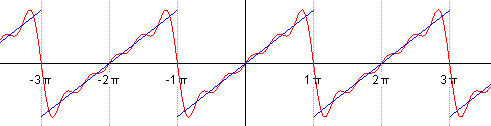
Практическое применение в современном мире
А вообще нужны ли эти ряды сейчас? Где они могут применяться практически и использует ли их кто-то кроме математиков-теоретиков? Оказывается, Фурье потому и знаменит на весь мир, что практическая польза его рядов буквально неисчислима. Их удобно применять там, где есть какие-либо колебания или волны: акустика, астрономия, радиотехника и т. д. Самый простой пример его использования: механизм работы фотоаппарата или видеокамеры. Если объяснять вкратце, эти устройства записывают не просто картинки, а коэффициенты рядов Фурье. И работает это везде – при просмотре картинок в интернете, фильма или прослушивании музыки. Именно благодаря рядам Фурье вы сейчас можете прочитать эту статью со своего мобильного телефона. Без преобразования Фурье нам не хватило бы никакой пропускной способности интернет-соединений, чтобы просто посмотреть видео на YouTube даже в стандартном качестве.
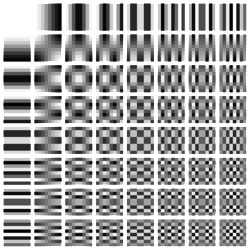
На этой схеме двухмерное преобразование Фурье, которое используется для разложения изображения на гармоники, т. е. базисные составляющие. На этой схеме черным закодировано значение -1, белым 1. Вправо и вниз по графику увеличивается частота.
Разложение в ряд Фурье
Наверное, вы уже устали читать, поэтому перейдем к формулам.
Для такого математического приема, как разложение функций в ряд Фурье, придется брать интегралы. Много интегралов. В общем виде ряд Фурье записывают в виде бесконечной суммы:
где
Если мы каким-то образом сможем посчитать бесконечное количество и (они и называются коэффициентами разложения Фурье, - это просто постоянная этого разложения), то полученный ряд в результате будет на 100% совпадать с исходной функцией на отрезке от до . Такой отрезок обусловлен свойствами интегрирования синуса и косинуса. Чем больше , для которого мы рассчитаем коэффициенты разложения функции в ряд, тем точнее будет это разложение.
Возьмем простую функцию
И так далее. В случае с такой функцией мы можем сразу сказать, что все , коэффициенты придется вычислять. Если мы возьмем первые четыре члена разложения в ряд Фурье для функции , получим:
График получившейся функции будет выглядеть следующим образом:
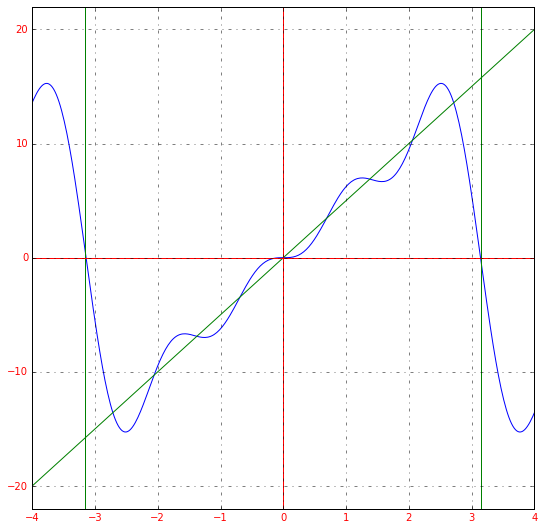
Получившееся разложение в ряд Фурье приближается к нашей исходной функции. Если мы возьмем большее количество членов ряда, например, 15, то увидим уже следующее:
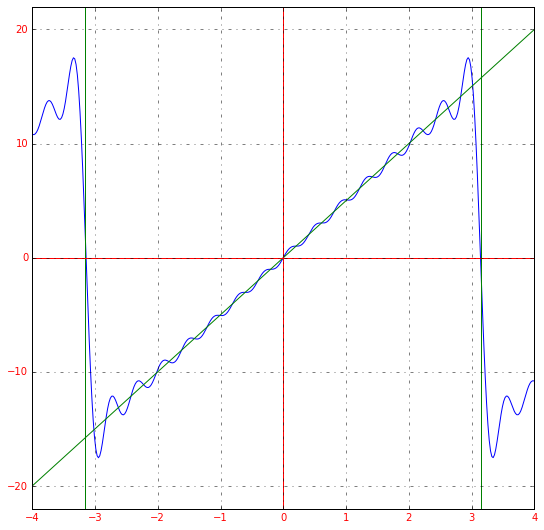
Чем больше членов разложения в ряд, тем выше точность.
Если мы немного изменим масштаб графика, сможем заметить еще одну особенность преобразования: ряд Фурье – это периодическая функция с периодом .
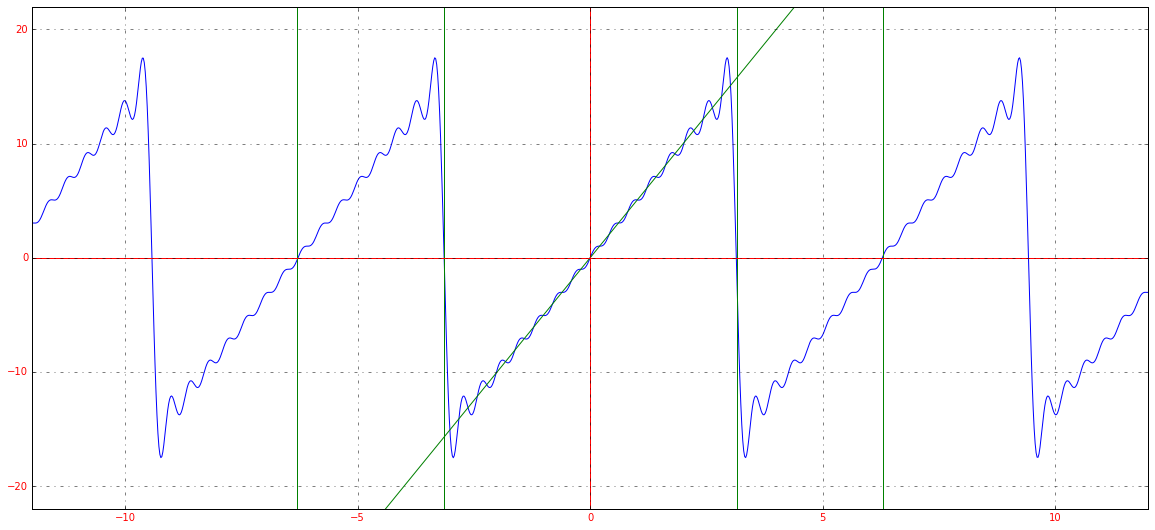
Таким образом, можно представлять любую функцию, которая является непрерывной на отрезке . Все это нужно для того, чтобы облегчить анализ каких-то явлений, которые описываются сложными функциями. Не всегда возможно аналитически (т. е. по формуле) посчитать производную, а в случае с набором синусов и косинусов такой проблемы не возникнет. Собственно разложение в ряд Фурье показывает, что зачастую задачи можно решать аналитически на упрощенных моделях, одним из примеров которых и является ряд Фурье.
Нужна работа по низкой цене? У нас вы можете заказать статью по физике недорого!



Комментарии 1
Спасибо за пояснения!! Хотелось бы только ещё больше примеров