Кому принадлежит уравнение Клапейрона-Менделеева?
Процесс преобразования вещества из жидкой или твердой фазы в газообразную, который происходит исключительно со свободной поверхности.
Известно, что скорость испарения зависит от площади свободной поверхности вещества, температуры и поверхностных оттоков.
Представление испарения при помощи цикла Карно
Для получения количественных характеристик процесса кроме молекулярно-кинетического метода используется термодинамический метод циклов, основанный С. Карно. Проведем по этому методу исследования преобразования жидкости в пар, связывая этот процесс с циклом Карно.
Предположим, что в цилиндре под поршнем находится в термодинамическом равновесии жидкость с ее насыщенным паром.
Осуществим с этой системой цикл Карно:
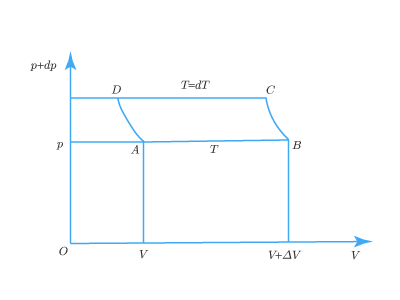
- Изотермическое расширение при температуре . Пусть при этом система получит количество теплоты, численно равное удельной теплоте парообразования , благодаря чему испарится дополнительно единица массы жидкости; объем системы увеличится на:
,
где – удельный объем жидкости, – удельный объем пара; давление насыщенного пара останется неизменным, поэтому этот процесс будет одновременно изобарическим;
2. Осуществим дальнейшее квазистатическое адиабатическое расширение , благодаря чему температура снизится до .
3. Изотермическое сжатие при – часть пара сконденсируется и выделится количество теплоты , которое будет передано телу с температурой .
4. Адиабатическое сжатие на бесконечно малый объем .
Цикл завершен, работа цикла равна площади :
.
Уравнение Клапейрона-Клаузиуса
По первому принципу термодинамики:
Учитывая, что коэффициент полезного действия цикла Карно не зависит от природы рабочего вещества, получим:
Поскольку в рассматриваемом цикле оперировали удельными величинами, в соответствии с их обозначениями из последних равенств получим:
Итак,
Последнее выражение называют уравнением Клапейрона-Клаузиуса. Это уравнение в 1834 предложил французский ученый Б. Π. Э. Клапейрон, а в 1850 г. его усовершенствовал немецкий физик Р. Ю. Э. Клаузис.
Оно подтверждается для произвольных фазовых переходов первого рода – испарения, плавления, сублимации и т.д.; отражает связь между изменениями равновесной температуры фазового перехода и равновесного давления насыщенного пара.
Найти удельную теплоту испарения жидкого азота при температуре -196 °С, если давление насыщенных паров азота при температурах -195, -196, -197 °С соответственно равно 111; 99; 88 кПа. Считать, что газообразный азот до температуры конденсации описывается уравнением Клапейрона-Менделеева. Удельным объемом жидкого азота пренебречь по сравнению с удельным объемом газообразного азота.
Учитывая, что значительно меньше , из уравнения Клапейрона-Клаузиуса находим:
По уравнению Клапейрона-Менделеева для единицы массы = 1 газообразного азота имеем:
Итак,
Перейдя в выражении от до конечных разностей , получим
После подстановки в уравнение численных данных получим = 2,09·105 (Дж/кг).
Не получается самостоятельно разобраться с темой? Заказать написание статьи по физике!



Комментарии