В статье Понятие вектора мы сказали, что векторы можно складывать друг с другом. Рассмотрим этот вопрос подробнее.
Пусть нам даны два вектора и . Что понимать под суммой этих двух векторов, то есть под ? Во первых, сумма двух векторов это вектор. То есть, если мы складываем два вектора (две стрелки) то снова получаем вектор (стрелку). Существуют два способа (или правила) как можно складывать векторы. Они, конечно, дают один и тот же самый результат. Говорят о правиле треугольника и правиле параллелограмма. Оба эти правила графические, то есть сумма векторов находится путем геометрического построения. О сумме векторов, выраженной через координаты векторов речь пойдет в другой статье.
Правило треугольника
Вот нам даны два вектора и . Для того чтобы найти их сумму, пользуясь правилом треугольника, нужно чтобы начало одного из векторов находилось в точке конца другого вектора. То есть, чтобы точки начала одного вектора и конца другого вектора совпадали. Но что делать, если это не так? Для этого нужно параллельно перенести любой из векторов так чтобы это условие выполнялось. Например, пусть вначале векторы у нас расположены так:

Перенесем теперь вектор параллельно самому себе так чтобы его начало совпало с концом вектора . Получим:
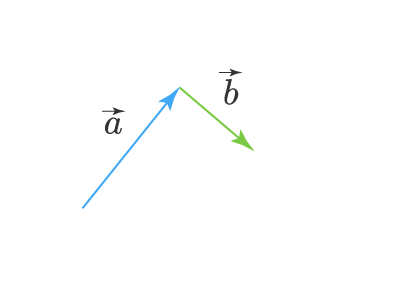
Теперь, чтобы найти сумму этих векторов, нужно провести вектор (стрелку) из начала вектора в конец вектора . Получим вектор :
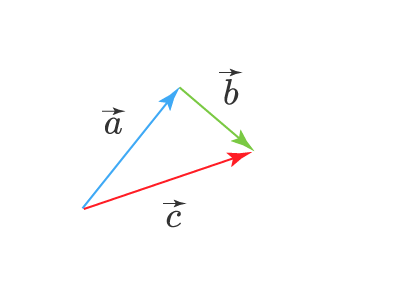
Правило параллелограмма
Решим ту же задачу вторым способом. Для этого нам нужно сделать так чтобы векторы и исходили из одной точки, то есть, чтобы точки начала этих векторов совпали. Получим:
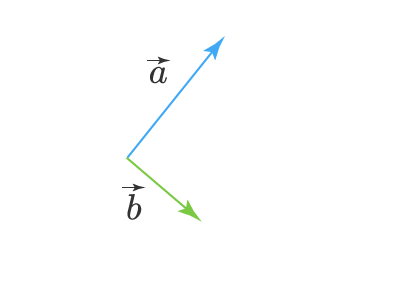
Теперь построим на этих двух векторах параллелограмм. Суммой векторов и будет вектор, совпадающий с диагональю этого параллелограмма, и начало этого суммарного вектора будет совпадать с началом векторов и :
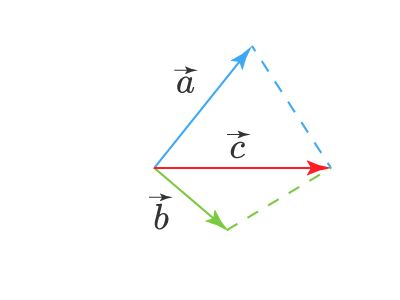
На самом деле, по своему смыслу, оба эти правила это одно и то же правило. Просто так уж вышло, что в зависимости от построения треугольника или параллелограмма, говорят о соответствующем правиле складывания векторов.
Сумма любого числа векторов
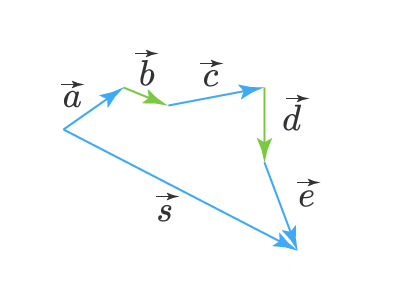
Складывать между собой можно не только два вектора, но и любое их количество. Для этого удобно воспользоваться правилом треугольника. Пусть у нас есть векторы . Пусть мы перенесли параллельно векторы так, что начало каждого последующего вектора берет свое начало в конце предыдущего вектора, тогда сумма этих векторов, вектор — это вектор с началом, совпадающим с началом первого вектора (вектора ) и концом, совпадающим с концом последнего вектора (вектора ):
Не знаете, где заказать написание статьи по математике на заказ? Авторы Студворк к вашим услугам!



Комментарии