Производная натурального логарифма

Найдем производную функции $f(x)= \ln x$ и приведем некоторые ее свойства и практические примеры использования.

Производная функции f(x)= ln x

Как известно, производной функции $f(x)$, определенной в точке $x_0$ и в некотором интервале, содержащем $x_0$, называют предел следующего вида:

$f^{'}(x_0)=\dfrac{df}{dx}\Bigr|_{x=x_0}=\lim\limits_{\Delta x \to 0}\dfrac{ f(x_0+ \Delta x)-f(x_0 )}{ \Delta x}$

если только такой предел существует.

Таким образом, для вычисления производной функции $f(x)$ необходимо последовательно:

1. Записать выражение для приращения функции:

$\Delta f(x_0 )=f(x_0+\Delta x)-f(x_0 )$

1. Упростить, по возможности, дробь

$\dfrac {\Delta f(x_0)}{\Delta x}=\dfrac {f(x_0+\Delta x)-f(x_0)}{\Delta x}$

1. Вычислить предел дроби при $\Delta x \to 0$ и записать полученное выражение для производной.

Применим этот алгоритм к вычислению производной натурального логарифма:

1. Записываем приращение функции:

$\Delta f(x_0)= f(x_0+\Delta x)-f(x_0)= \ln (x_0+\Delta x)-\ln {x_0}=\ln \dfrac { x_0+\Delta x }{ x_0}$

1. Получаем дробь:

$\dfrac {\Delta f(x_0)}{\Delta x}= \dfrac {1}{\Delta x} \cdot \ln {\dfrac {x_0+\Delta x }{ x_0}}=\ln {\Bigl( 1+\dfrac {\Delta x }{ x_0} \Bigr)}^ {\dfrac {1}{\Delta x}}=\dfrac {1}{x_0} \ln {\Bigl( 1+\dfrac {1 }{ x_0 / \Delta x } \Bigr)}^{ \dfrac {x_0}{\Delta x}}$

1. Вычисляем производную:

$f'(x_0 )=\lim\limits_{\Delta x \to 0} \Bigl( \dfrac {1}{ x_0} \ln {\Bigl( 1+\dfrac {1 }{ x_0 / \Delta x } \Bigr)}^{ \dfrac {x_0}{\Delta x}}\Bigr) =\dfrac {1}{ x_0} \cdot \lim\limits_{\Delta x \to 0} \ln {\Bigl( 1+\dfrac {1 }{ x_0 / \Delta x } \Bigr)}^{ \dfrac {x_0}{\Delta x}}=\dfrac {1}{ x_0} \cdot \ln \lim\limits_{\Delta x \to 0} {\Bigl( 1+\dfrac {1 }{ x_0 / \Delta x } \Bigr)}^{ \dfrac {x_0}{\Delta x}}$

Для вычисления предела

$\lim\limits_{\Delta x \to 0} {\Bigl( 1+\dfrac {1 }{ x_0 / \Delta x } \Bigr)}^{ \dfrac {x_0}{\Delta x}}$

обозначим:

$\dfrac {x_0}{ \Delta x }=n$

Учитывая, что $n\to\infty$ при условии, что $\Delta x \to 0$, получаем:

$\lim\limits_{\Delta x \to 0} {\Bigl( 1+\dfrac {1 }{ x_0 / \Delta x } \Bigr)}^{ \dfrac {x_0}{\Delta x}}=\lim\limits_{n\to\infty } {\Bigl( 1+\dfrac {1 }{n} \Bigr)}^{ n}$

Полученный предел является одним из представлений экспоненты, числа $e≈2, 71828$ (число Непера или число Эйлера):

$e=\lim\limits_{n\to\infty } {\Bigl( 1+\dfrac {1 }{n} \Bigr)}^{ n}$

Тогда, искомая производная равна:

$f'(x_0) =\dfrac {1}{ x_0} \cdot \ln \lim\limits_{\Delta x \to 0} {\Bigl( 1+\dfrac {1 }{ x_0 / \Delta x } \Bigr)}^{ \dfrac {x_0}{\Delta x}}=\dfrac {1}{ x_0}\cdot \ln e=\dfrac {1}{ x_0}$

Таким образом:

$f'(x)=(\ln x) '=\dfrac {1}{ x}$

Некоторые свойства и практические примеры

1. Приведем правило для нахождения производной обратной функции.

Пусть дана функция $y=f(x)$, в которой переменная x является аргументом. Полагая теперь аргументом переменную y, получим функцию в виде $x=g(y)$.

Очевидно, что $f(g(y))=y$ или $f(g(x))=x$. Такую функцию $g(x)$ называют обратной для $f(x)$. Производную обратной функции можно найти по правилу:

$y_x'=\dfrac {dy}{dx}=\dfrac {1}{\dfrac {dx}{dy}}=\dfrac {1}{x_y'}$

Пример 1

Используя правило для обратной функции найти производную функции $f(x)= \ln{x}.$

Решение

Заметим, что обратной для логарифмической функции $\ln{x}$ является показательная функция $e^x$. Действительно:

$f(g(x)) = \ln {e^x} = x$

Воспользуемся далее формулой для производной экспоненты:

$(e^{x})^{'}=e^{x}$

Получаем:

$y_x' = (\ln {x})' = \dfrac {1}{(e^{y})^{'}_y}= \dfrac {1}{e^y}= \dfrac {1}{e^{\ln x}}= \dfrac {1}{x}$

Как и следовало ожидать, результат совпадает с полученным ранее.

1. Угол наклона $\alpha$ касательной к графику функции $y= \ln {x}$ в точке $x=x_0$ определяется соотношением:

$\tg \alpha =y^{'} (x_0 )= \dfrac {1}{x_0}$

Здесь угол $\alpha$ это угол между касательной и осью $Ox$ отсчитываемый от положительного направления $Ox$ против часовой стрелки.

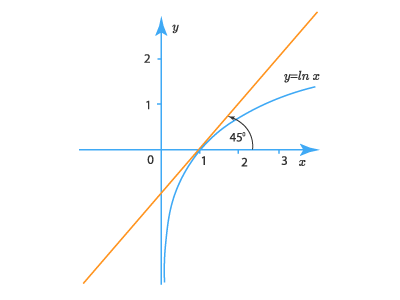
Производная функции $f(x)= \ln {x}$ в точке $x_0=1$ равна $1$:

$f' (x_0 ) = (\ln {x})_{x_0=1}^{'}=\dfrac {1}{1}=1$

Это означает, что касательная к графику в точке $M(1;0), (x_0=1, y_0=\ln {1} = 0)$ составляют с осью $Ox$ угол $45° (\tg {45°}=1)$

1. Производная сложной функции $y=\ln {g(x)}$ согласно правил дифференцирования, равна:

$y'=g'(x) \dfrac {1}{g(x)}$

1. Производная сложной функции $y=u(v)$, где $v= \ln {x}$ равна:

$y'=u'_v \cdot v'=u'_v \cdot \dfrac {1}{x}$

Пример 2

Найти производную функции $f(x)=\ln {(x^2+2x)}$

Решение

$f'(x)=(\ln {(x^2+2x)})'=(x^2+2x)' \cdot \dfrac {1}{x^2+2x}=\dfrac {2x+2}{x^2+2x}$

Пример 3

Найти производную функции

$f(x)= \sin {(\ln {2x})}$

Решение

Полагаем $\ln {2x}=v$

Тогда:

$f'(x)=(\sin {v})'_v \cdot v' = \cos {v} \cdot (\ln {2x})' =\cos{(\ln {2x})} \cdot (2x)' \cdot \dfrac {1} {2x} = \dfrac {\cos(\ln{2x})} {x}$

Не знаете, где заказать написание статьи по математике на заказ? Авторы Студворк к вашим услугам!

Тест по теме «Производная натурального логарифма»