Простейшие свойства факториала и гамма-функции

Настоящая статья начинает подраздел, в котором рассматриваются функции $\mathbf{\Pi}(z)$, $\Gamma(z)=\mathbf{\Pi}(z-1)$ и связанные с ними функции $\Psi(z)$ и $\psi(z)=\Psi(z-1)$, а также функции, определяемые как суммы обратных степеней – $\zeta(z)$ (дзета-функция Римана) и $\beta(z)$.

Из высших трансцендентных функций (т.е. трансцендентных функций, не являющихся элементарными) функции $\Gamma(z)$ и $\psi(z)$ являются одними из наиболее простых.

Данные функции используются для представления и вычисления некоторых определенных интегралов и сумм.

Функция $\mathbf{\Pi}(z)=\Gamma(z+1)$ является обобщением факториала $\mathbf{\Pi}(n)=n!$,
который в элементарной математике определяется для целых неотрицательных чисел простой формулой

$n! =\prod_{k=1}^{n} k \;.$

Кроме того, функция $\Gamma(z)$ используется во многих уравнениях для гипергеометрических функций (см. подраздел «Гипергеометрические функции»); поэтому, можно сказать, изучение гипергеометрических функций невозможно без предварительного изучения гамма-функции.

В настоящей статье даны определения функций, которые рассматриваются далее, и качественно описан характер их поведения.

Определения основных функций

Функции $\mathbf{\Pi}(z)$ (факториал или пи-функция) и $\Gamma(z)=\mathbf{\Pi}(z-1)$ (гамма-функция) удобнее всего определить с помощью формулы

$\mathrm{Ln}\,\mathbf{\Pi}(z) =\lim_{M\to \infty} \Bigl(z\cdot \ln M -\sum_{k=1}^{M} \ln(1+z/k)\Bigr) \;.$

Другие формы записи данного соотношения

$1/\mathbf{\Pi}(z) = \lim_{M\to \infty} M^{-z}\cdot \prod_{k=1}^{M} (1+z/k) \qquad (|z|<\infty) \;,$

$1/\mathbf{\Pi}(z) = \lim_{M\to \infty} \frac{ M^{-z} }{M!}\cdot \prod_{k=1}^{M} (z+k) \qquad (|z|<\infty) \;.$

Здесь $\mathrm{Ln}\,\mathbf{\Pi}(z)$ – функция, которая для комплексных значений аргумента рассматривается наряду с функцией $\mathbf{\Pi}(z)$, и значение которой для каждого значения $z$ равно $\mathrm{Ln}\,\mathbf{\Pi}(z) =\ln\mathbf{\Pi}(z) +2 \,\pi \,k$, где $k$ – некоторое целое число, определяемое таким образом, чтобы функция $\mathrm{Ln}\,\mathbf{\Pi}(z)$ непрерывно зависела от $\mathrm{Im}\, z$. Аналогично, для комплексных значений аргумента наряду с функцией $\Gamma(z)$ рассматривается функция $\mathrm{Ln}\,\Gamma(z)$.

Функции $\Psi(z)$ и $\psi(z)=\Psi(z-1)$ (\emph{дигамма-функция} или \emph{пси-функция}) определяются как логарифмические производные, соответственно, функций $\mathbf{\Pi}(z)$ и $\Gamma(z)$:

$\Psi(z) =\frac{d}{d z} \,\mathrm{Ln}\,\mathbf{\Pi}(z) \;,\qquad \psi(z) =\frac{d}{d z} \,\mathrm{Ln}\,\Gamma(z) \;.$

Из определения сразу следует следующее представление функции $\Psi(z)$:

$\Psi(z) =\lim_{M\to \infty} \Bigl(\ln M -\sum_{k=1}^{M} (z+k)^{-1}\Bigr) \;.$

В качестве альтернативных определений функций $\mathbf{\Pi}(z)$ и $\Psi(z)$ иногда используются представления данных функций в виде некоторых сходящихся рядов или определенных интегралов (см. статьи «Представление гамма-функции и связанных с ней функций в виде сходящихся рядов» и «Интегральные представления гамма-функции и связанных с ней функций»).

Особые точки

a) Особыми точками функции $\mathbf{\Pi}(z) =\Gamma(z+1)$ в открытой комплексной плоскости являются числа $z_k=-k$ \ $(k=1,2,3,...)$. Каждая из точек $z_k$ является простым полюсом с вычетом

$\mathrm{res}_{z_k} \mathbf{\Pi}(z) =\lim_{z\to -k} (z+k)\cdot \mathbf{\Pi}(z) =\frac{ (-1)^{k-1} }{(k-1)!} \;.$

b) Особыми точками функции $\Psi^{(m)}(z) =(d /d z)^{m+1} \,\mathrm{Ln}\,\mathbf{\Pi}(z) =(d /d z)^{m+1} \,\mathrm{Ln}\,\Gamma(z+1)$
\ ($m =0,1,2,...$) в комплексной плоскости являются числа $z_k =-k$ \ ($k=1,2,3,...$).

Для функции $\Psi^{(0)}(z) =\Psi(z)$ каждая из точек $z_k$ является простым полюсом с вычетом

$\mathrm{res}_{z_k} \Psi(z) =-1 \;.$

Для функции $\Psi^{(m)}(z)$ при $m>0$ каждая из точек $z_k$ является полюсом порядка $m+1$ с вычетом

$\mathrm{res}_{z_k} \Psi^{(m)}(z) =\lim_{z \to -k} (z+k)\cdot \Psi^{(m)}(z) =0 \;.$

Фазовые соотношения

$\mathbf{\Pi}(x)(z^*) =\bigl(\mathbf{\Pi}(x)(z)\bigr)^* \;,\qquad \Psi(z^*) =\bigl(\Psi(z)\bigr)^* \;.$

Факториал действительного аргумента

Множеством значений функции $y=\mathbf{\Pi}(x)$ является множество отличных от нуля действительных чисел. В точках $x_k=-k$ \ $(k=1,2,...)$ функция терпит разрыв. Нулей не имеет.

На рисунке 1 представлены графики функций $y=\mathbf{\Pi}(x)$ (сплошная кривая) и $y=1/\mathbf{\Pi}(x)$ (пунктирная кривая).

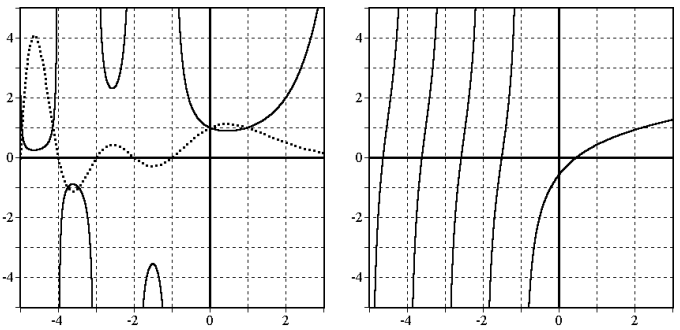
Рис. 1. Графики функций $\mathbf{\Pi}(x)$ (сплошная кривая) и $1/\mathbf{\Pi}(x)$ (кривая из точек).

Рис.2. График функции $\Psi(x)$.

Дигамма-функция действительного аргумента

Множеством значений функции $y=\Psi(x)$ является множество действительных чисел. В точках $x_k=-k$ \ $(k=1,2,...)$ функция терпит разрыв. В интервалах $[-1,+\infty]$ и $[-k-1,-k]$ \ $(k=1,2,...)$,
ограниченных точками разрыва, функция возрастает; в каждом из данных интервалов она имеет единственный нуль.

На рисунке 2 представлен график функций $y=\Psi(x)$.

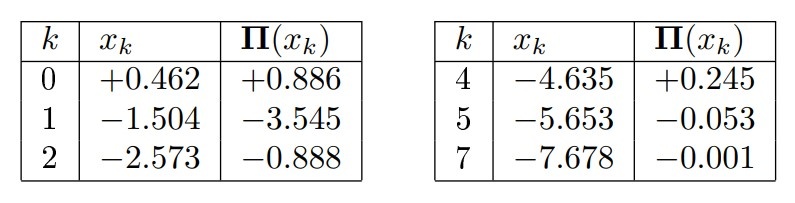
В следующей таблице представлены нули функции $\Psi(x)$ и соответствующие экстремальные значения функции $\mathbf{\Pi}(x)$:

Литература

1. Под ред. М. Абрамовица, И. Стиган. Справочник по специальным функциям с формулами, графиками, математическими таблицами. – Москва, «Наука», 1979, 830 с. Перевод с английского: Edited by M. Abramowitz and I.A. Stegun. Handbook of Mathematical Functions with formulas, graphs and mathematical tables. – National bureau of standards. Applied mathematics series – 55, 1964.

2. Г.Бейтмен, А.Эрдейи. Высшие трансцендентные функции, т. 1. СБМ.
   Высшие трансцендентные функции, т. 1. Гипергеометрическая функция. Функции Лежандра. – Москва, «Наука», 1973; 297с.
   Перевод с английского: H. Bateman, A. Erdelyi. Higher Transcendental Functions, Volume 1. MC Graw-Hill Book Company, Inc., New York - Toronto - London, 1953.

3. http://www.wolfram.com – Internet-page of the firm WolframResearch.

4. А.Ф. Никифоров, В.Б. Уваров. Специальные функции математической физики. – Москва, «Наука», 1984, 344 с.

5. А.П. Прудников, Ю.А. Брычков, О.И. Маричев. Интегралы и ряды. Элементарные функции. – Москва, «Наука», 1981, 800 с.

6. А.П. Прудников, Ю.А. Брычков, О.И. Маричев. Интегралы и ряды. Специальные функции. – Москва, «Наука», 1983, 752 с.

7. А.П. Прудников, Ю.А. Брычков, О.И. Маричев. Интегралы и ряды. Дополнительные главы. – Москва, «Наука», 1986, 800 с.

8. Е. Янке, Ф. Эмде, Ф. Леш. Специальные функции. – Москва, «Наука», 1968, 344 с. Перевод с немецкого: E. Janke, F. Emde, F. Lösch. Tafeln Höherer Funktionen. B.G. Teubner–Verlagsgesellschaft–Stuttgart, 1960, 344 p.

Нужна работа по низкой цене? У нас вы можете заказать статью по математике недорого!